Предмет: Математика,
автор: meliksetanartem5
решите систему уравнений
Приложения:
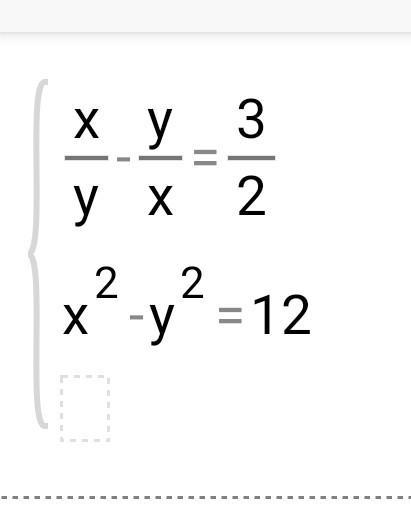
Ответы
Автор ответа:
0
Ответ:
(-4; -2) и (4; 2)
Пошаговое объяснение:
подставляем во второе, получим
пусть z=y², получаем
по теореме Виета
z₁ +z₂=-12
z₁ * z₂ = -64
z₁ = -16; z₂ = 4
z₁ = -16 не имеет смысла
y² = 4 ⇒ у =±2
тогда
Похожие вопросы
Предмет: Українська література,
автор: liza11223344
Предмет: Математика,
автор: FINE333
Предмет: Математика,
автор: Lepesevich78
Предмет: Математика,
автор: Ucoba