Предмет: Геометрия,
автор: gagepyq
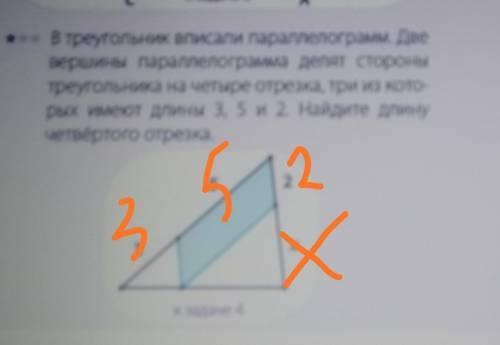
В треугольник вписали параллелограмм. Две вершины параллелограмма делят стороны треугольника на 4 отрезка, три из которых имеют длины 3, 5 и 2. Найдите длину четвёртого отрезка.
Приложения:
Ответы
Автор ответа:
13
Ответ:
ед.
Объяснение:
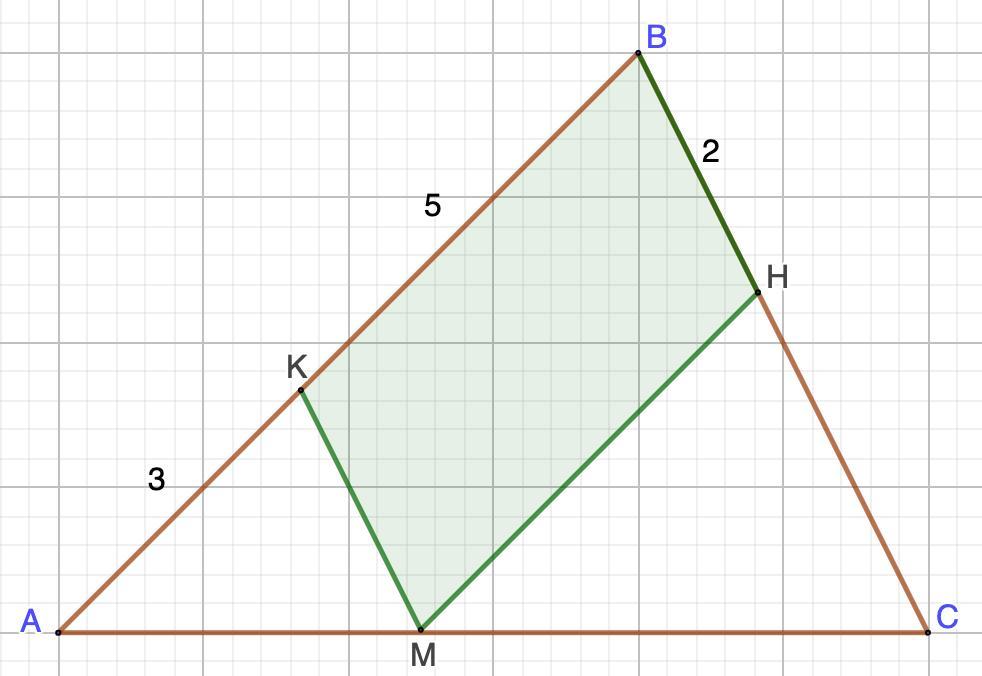
Дано: ΔАВС.
MKВН - параллелограмм, вписанный.
АК = 3; КВ = 5; ВН = 2.
Найти: НС.
Решение:
1. Рассмотрим ΔМАК и ΔАВС.
- У параллелограмма противоположные стороны параллельны.
⇒ МК || ВС.
- У параллелограмма противоположные стороны равны.
⇒ МК = ВН = 2
- Лемма. Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.
⇒ ΔМАК ~ ΔАВС.
Составим пропорцию и найдем ВС:
⇒ НС = ВС - НВ
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Katynapopova
Предмет: Математика,
автор: aggul
Предмет: Физика,
автор: saysanova00
Предмет: Математика,
автор: flag4
Предмет: Обществознание,
автор: maloyzolotov