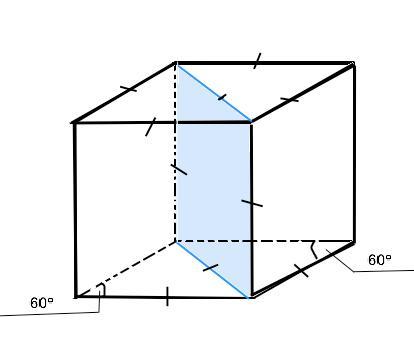
Основанием прямой призмы является ромб со стороной 12 см и углом 60°. Меньшее из диагональных сечений призмы является квадратом. Найдите объем призмы.
Ответы
V=Sосн.*h
Sосн=a²*sinA
S=12²*√2/2=72√2см²
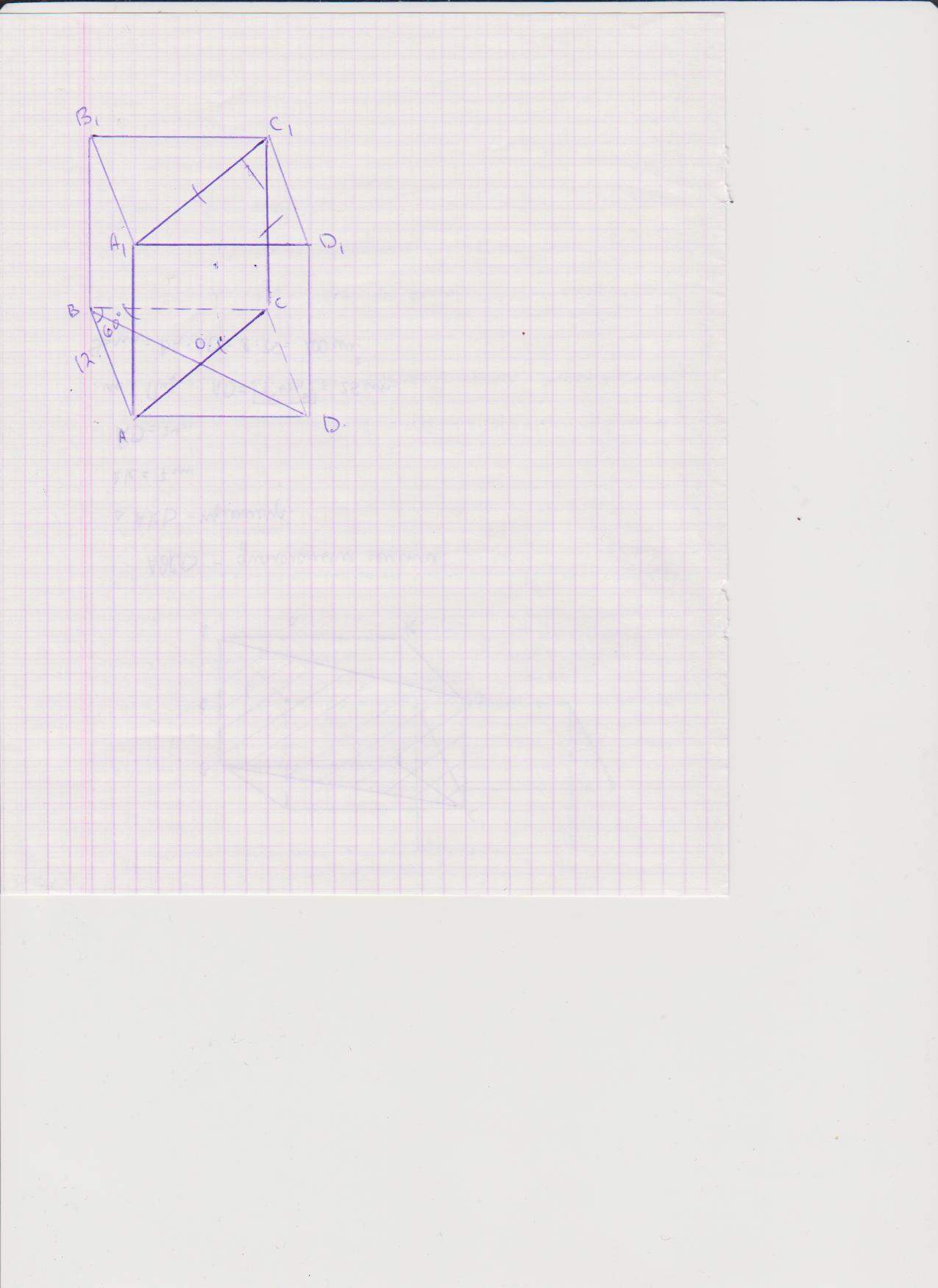
из треугольника АBO-прямоугольный, <B=30=> AO=1/2BA=6см
=> BD=12см, тк.BB1DD1-квадрат BD=BB1=12 cм
V=72√2*12=864√2 см^3
Ответ: 864√3 см³
Объяснение:
Так как основание призмы ромб с острым углом 60°, меньшая диагональ делит его на два равносторонних треугольника с равными углами при их основании ( меньшей диагонали). Поэтому высота призмы равна этой диагонали как сторона квадратного сечения, т.е. h=12 см. Объём призмы находят произведением площади основания на высоту ромба.
V=S•h.
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними. Ромб - параллелограмм с равными сторонами. S=a²•sin60°=12²•√3/2=72√3 см² ⇒
V=72√3•12=864√3 см³