Срочно, пожалуйста помогите
Ответы
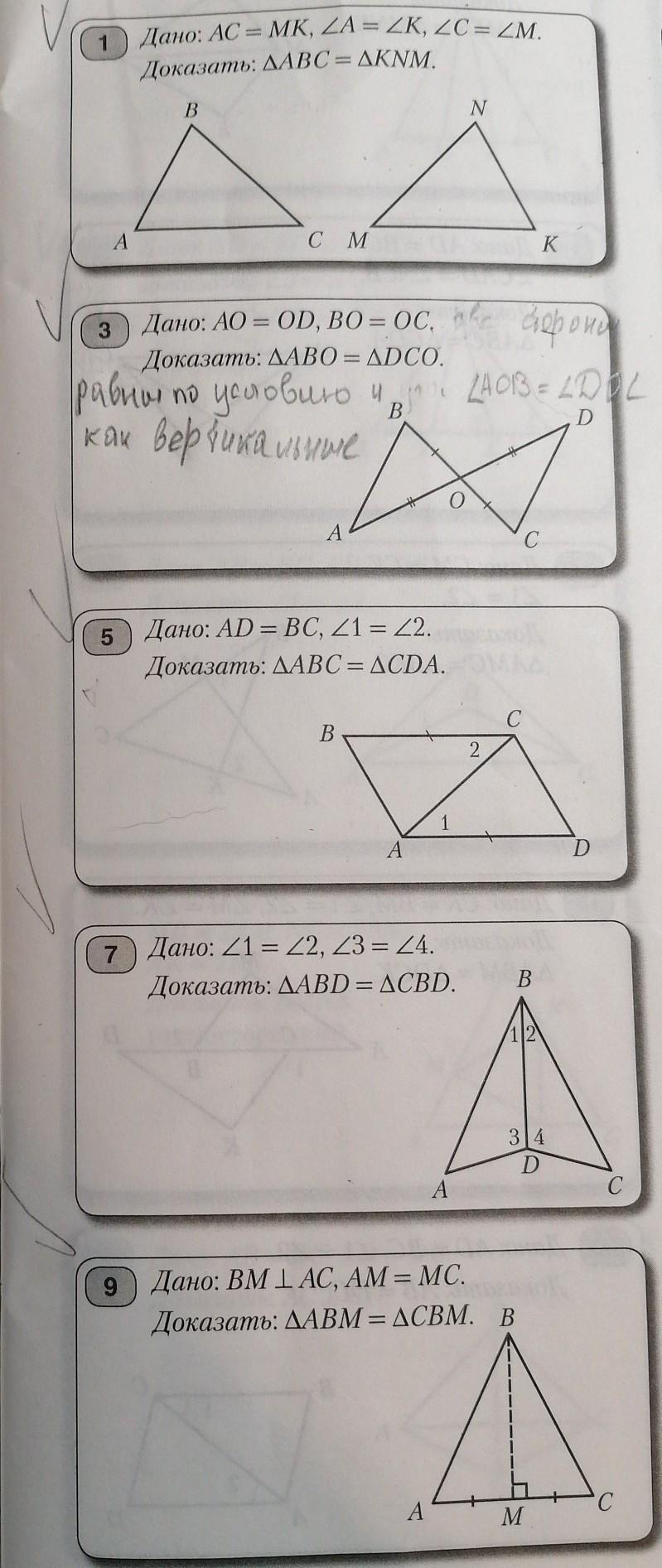
Ответ:Номер 1
По условию задачи основания треугольников равны между собой и прилежащие к основанию углы тоже равны между собой,поэтому мы можем утверждать ,что треугольник АВС
равен треугольнику MNK по второму признаку равенства треугольников-если одна сторона и два прилежащих к ней угла одного треугольника равны стороне и двум прилежащих к ней углам другого треугольника,то эти треугольники равны между собой
Задание 2
Опять же,согласно условию задачи,
Углы АОВ и DOC равны между собой,а также равны стороны
ВО=ОС. АО=ВD и поэтому мы можем утверждать,что треугольники АВО и ODC равны между собой на основании первого признака равенства треугольников-если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника,то эти два треугольника равны между собой
Задание 3
По условию-две стороны равны между собой и два угла равны между собой
А теперь не по условию,а по рисунку-,сторона СА-общая,поэтому согласно первому признаку равенства треугольников,когда две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними второго треугольника,то треугольники равны между собой
Задание 4
По условию задачи,угол 1 равен углу 2,а угол 3 равен углу 4
А по чертежу видно,что BD- общая сторона
По второму признаку равенства треугольников можно утверждать,что треугольник АВD равен треугольнику BDC
Задание 5
По условию: АМ=МС
Угол АМВ равен углу ВМС и каждый из них равен 90 градусов,т е являются прямыми углами,т к ВМ перпендикуляр на АС
ВМ является общей стороной
Поэтому по первому признаку равенства треугольников,треугольник АВМ равен ВМС,т к если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника,то треугольники равны между собой
Объяснение: