Предмет: Геометрия,
автор: makcmens
В трапеции ABCD BC и AD - основания, BC : AD = 3 : 5. Площадь трапеции равна 80 см2. Найдите площадь треугольника АВС
Ответы
Автор ответа:
0
Ответ:
Площадь треугольника АВС:
30 см²
Объяснение:
ВС : AD = 3 : 5
Пусть х - коэффициент пропорциональности, тогда
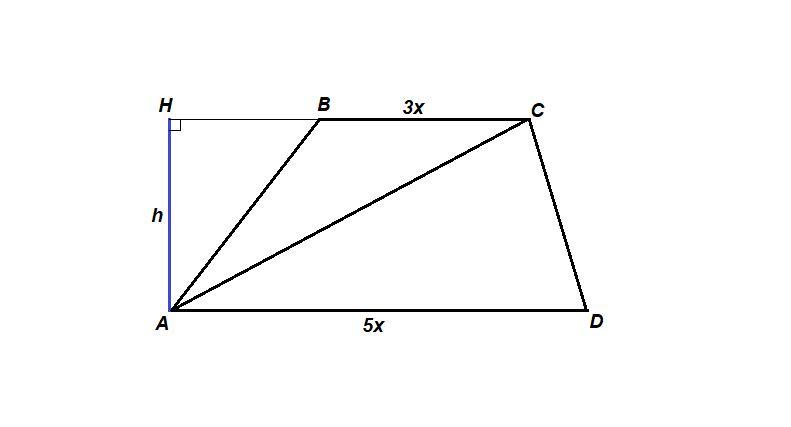
ВС = 3х, AD =5x.
Проведем высоту трапеции АН из вершины А.
АН также высота треугольника АВС, проведенная к продолжению стороне ВС.
Обозначим АН = h.
- Площадь трапеции равна произведению полусуммы оснований на высоту.
- Площадь треугольника можно найти как половину произведения стороны на проведенную к ней высоту.
см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: rastorgyeva3096
Предмет: Русский язык,
автор: bezuglaia
Предмет: Русский язык,
автор: oleinikva2006
Предмет: Математика,
автор: senyazer