Question

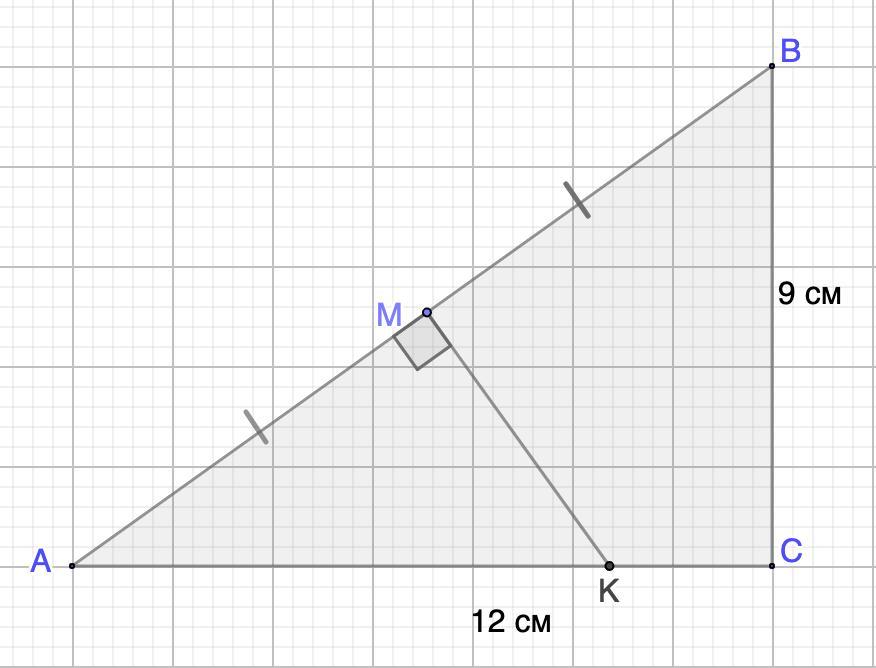
ABC – прямоугольный треугольник.
– прямой, AC=12 см, BC=9 см.
, где точка M – середина стороны AB, точка K расположена на стороне AC. Найди длину отрезка AK.
AK=
cм. НЕ ОБРАЩЯЕТЕ НА ЭТО. ВАПРОС НА ФОТО

Answer 1

Ответ:

9 3/8 см

Объяснение:

Дано: ΔАВС - прямоугольный.

АС = 12 см; ВС = 9 см.

МК ⊥ АВ; АМ = МВ.

Найти: АК

Решение:

1. Рассмотрим ΔАВС - прямоугольный.

По теореме Пифагора:

$AB^2 = AC^2+BC^2=144+81=225\\\\AB=\sqrt{225}=15\;_{(CM)}$

⇒   $\displaystyle AM = MB = 15:2 = \frac{15}{2} \;_{(CM)}$

2. Рассмотрим ΔАВС и ΔАМК - прямоугольные.

∠А - общий.

⇒ ΔАВС ~ ΔАМК ( по двум углам)

Составим пропорцию:

$\displaystyle \frac{AK}{AB}=\frac{AM}{AC}\\\\\frac{AK}{15}=\frac{\frac{15}{2} }{12} \\\\AK=\frac{15*15}{2*12}=\frac{75}{8}=9\frac{3}{8}\;_{(CM)}$