Предмет: Геометрия,
автор: geyskayadevka
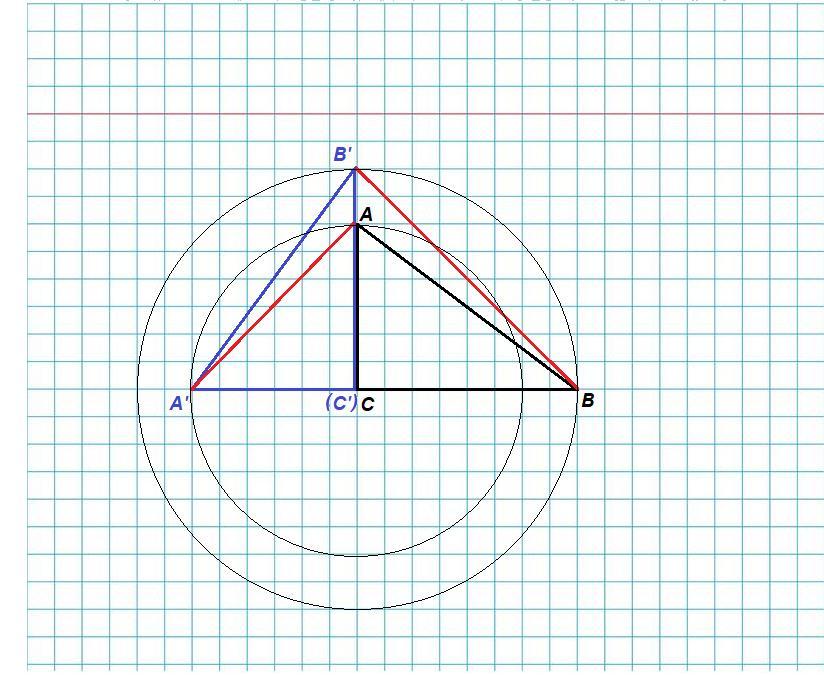
Совершили поворот треугольника ABC вокруг вершины С на 90 градусов против часовой стрелки и получили треугольник A'B'C'. Если AC=11 см,BC=12см то почему равны длины отрезков АА' и BB'.
ПОМОГИТЕ, СРОЧНО
Ответы
Автор ответа:
1
Ответ:
AA' = 11√2 см
BB' = 12√2 см
Объяснение:
При повороте катета АС на 90° вокруг точки С получается прямоугольный равнобедренный треугольник АA'C, в котором
А'C = AC = 11 см
По теореме Пифагора:
см
При повороте катета ВС на 90° вокруг точки С получается прямоугольный равнобедренный треугольник ВВ'C, в котором
В'C = ВC = 12 см
По теореме Пифагора:
см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: nastia15012002
Предмет: Алгебра,
автор: danaislyamova
Предмет: Геометрия,
автор: NnastyaIvanova
Предмет: Физика,
автор: камусик2004
Предмет: Математика,
автор: Rollipolli