Предмет: Геометрия,
автор: Candyman2
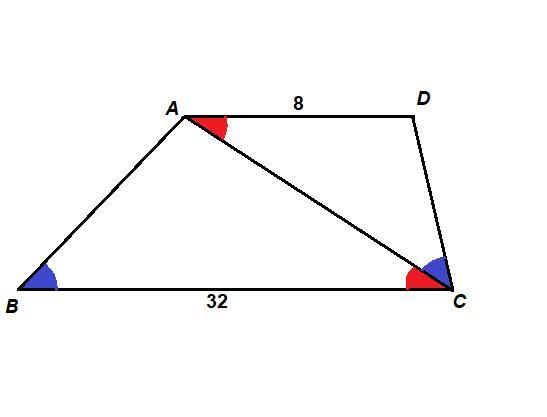
В трапеции ABCD с диагональю AC углы ABC и ACD равны. Найди диагональ AC, если основания BC и AD равны соотвественно 32 и 8 см.
16 см
18 см
19 см
15 см
Ответы
Автор ответа:
0
Ответ:
16 см
Объяснение:
∠ABC = ∠ACD по условию,
∠АСВ = ∠DAC как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АС, значит
ΔABC ~ ΔDCA по двум углам.
см
Приложения:
Похожие вопросы
Предмет: История,
автор: niksei1835
Предмет: История,
автор: dopstoevskiy
Предмет: Другие предметы,
автор: mfjsyt143
Предмет: Биология,
автор: ДенисРудых
Предмет: Биология,
автор: алек2205