Предмет: Геометрия,
автор: killuazolydick
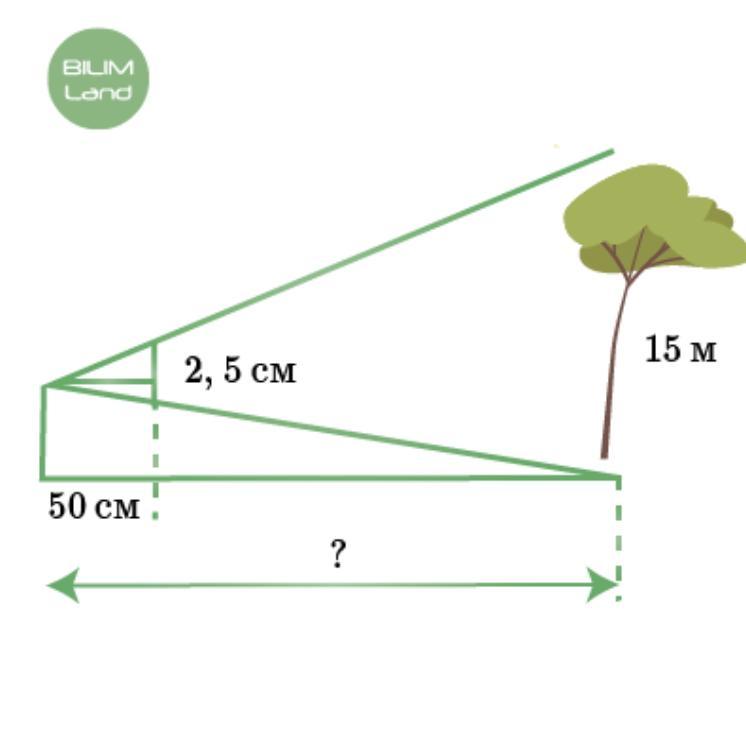
Если Азат держит копейку диаметром 2,5 см на растояний 50 см от глаза, то дерево высотой 15 м не видно. Найди растояние между Азатом и деревом.
Приложения:
Ответы
Автор ответа:
2
Ответ:
300 м
Объяснение:
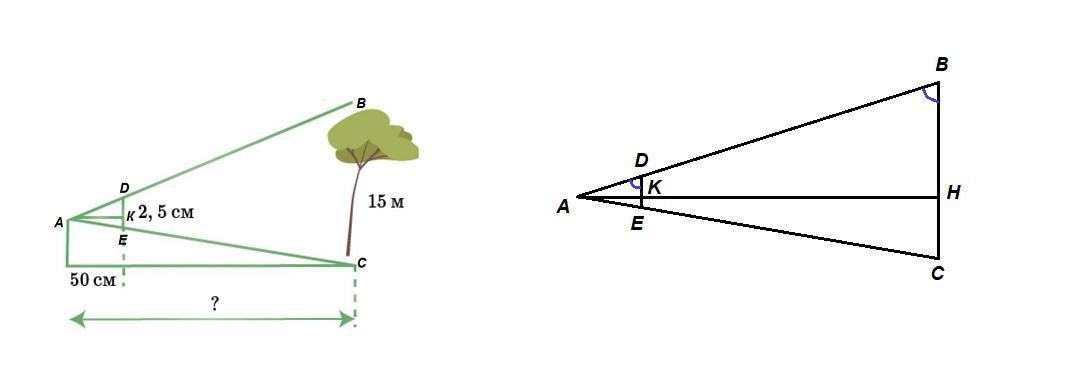
Обозначим:
А - глаза Азата,
ВС - дерево
АК = 50 см - расстояние от глаза до копейки
DE = 2,5 см - диаметр копейки
АН - расстояние от Азата до дерева - искомое.
Считаем, что копейка параллельна дереву.
∠ADE = ∠ABC как соответственные при пересечении параллельных прямых DE и ВС секущей АВ,
∠A - общий для треугольников ADE и АВC, значит
ΔADE ~ ΔABC по двум углам.
Отношение высот подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия:
15 м = 1500 см
см
АН = 30 000 см = 300 м
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Живчик11
Предмет: Алгебра,
автор: beibeibeiaisa
Предмет: Русский язык,
автор: 200623
Предмет: Математика,
автор: Русн6п6