Question

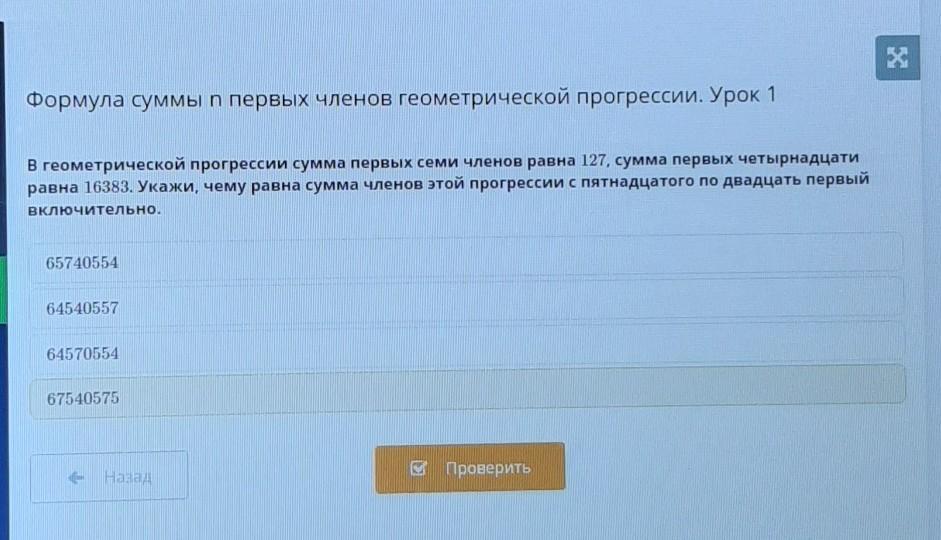
В геометрической прогрессии сумма первых семи членов равна 127, сумма первых четырнадцати
равна 16383. Укажи, чему равна сумма членов этой прогрессии с пятнадцатого по двадцать первый
включительно.​

Answer 1

Ответ:

Среди предложенных вариантов нужного нет, так как получается

2080768

Объяснение:

По условию

$\tt S_{7}=127, \;\; S_{14}=16383.$

Известно, что сумма первых n членов геометрической прогрессии определяется по формуле:

$\tt S_{n}=\dfrac{b_{1} \cdot (q^{n}-1)}{q-1}.$

Подставляем известные значения:

$\tt 127=\dfrac{b_{1} \cdot (q^{7}-1)}{q-1}\\\\16383=\dfrac{b_{1} \cdot (q^{14}-1)}{q-1}.$

Из первого уравнения определяем b₁ и подставим во второе уравнение:

$\tt b_{1} =\dfrac{127 \cdot (q-1)}{q^{7}-1}\\\\16383=\dfrac{\dfrac{127 \cdot (q-1)}{q^{7}-1} \cdot (q^{14}-1)}{q-1}.$

Упростим второе уравнение и находим знаменатель прогрессии q:

$\tt 16383=\dfrac{127 \cdot (q-1) \cdot (q^{14}-1)}{(q^{7}-1) \cdot (q-1) }\\\\16383:127=\dfrac{(q^{7}-1) \cdot (q^{7}+1)}{(q^{7}-1) }\\\\129=q^{7}+1\\q^{7}=128 \\q=2.$

Значение знаменателя прогрессии q=2 подставим в первое уравнение и находим b₁:

$\tt b_{1} =\dfrac{127 \cdot (2-1)}{2^{7}-1}=\dfrac{127 \cdot 1}{127}=1.$

Теперь остаётся найти сумму членов прогрессии с пятнадцатого по двадцать первый, включительно. Для этого находим разность S₂₁-S₁₄:

$\tt S_{21}-S_{14}=\dfrac{1 \cdot (2^{21}-1)}{2-1}-\dfrac{1 \cdot (2^{14}-1)}{2-1}=2^{21}-1-(2^{14}-1)=2^{21}-1-2^{14}+1=\\\\=2^{21}-2^{14}=2^{14} \cdot (2^{7}-1)=16384 \cdot 127=2080768.$