Question

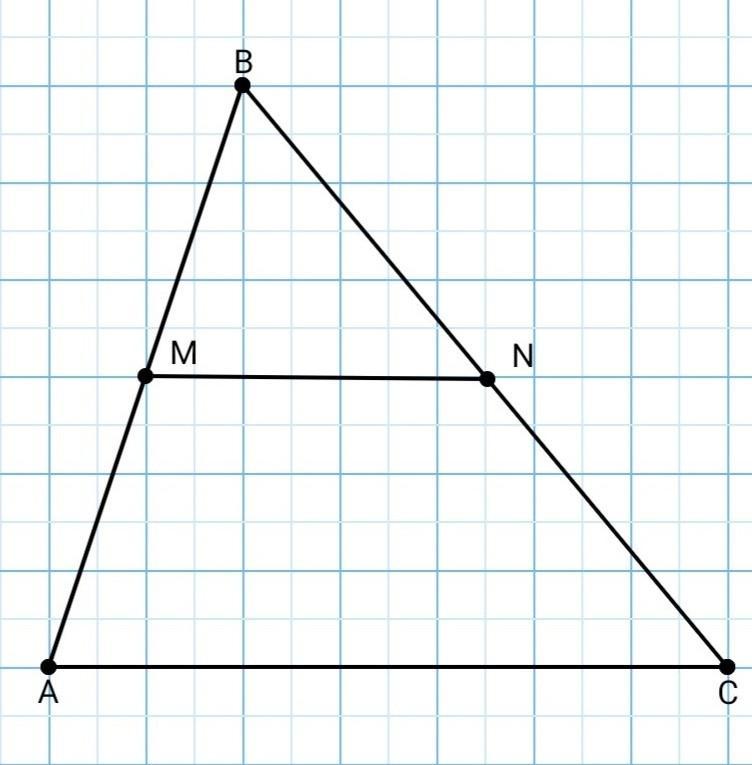
В треугольнике АВС точки M и N принадлежат соответственно сторонам АВ И ВС. Отрезок МN является средней длиной если:
А) MN || АС
Б) MN = 1:2 AC
B) MN = 1:2 AC, ∠BNM = ∠BAC
Г) MN = 1:2 AC, ∠BNM = ∠BСА
Все с подробным решением и объяснением. Заранее спасибо

Answer 1

Ответ: Г

Объяснение:

• Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника.

• Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника

Таким образом, для того, чтобы отрезок MN был средней линией треугольника АВС должны одновременно выполняться условия:

1. MN || АС
2. MN = 1:2 AC

А) MN || АС - выполняется только первое условие, MN- не средняя линия.

Б) MN = 1:2 AC - выполняется только второе условие, MN- не средняя линия.

B) MN = 1:2 AC, ∠BNM = ∠BAC - выполняется только второе условие, MN- не средняя линия.

Г) MN = 1:2 AC, ∠BNM = ∠BСА

Второе условие выполняется.

Рассмотрим выполнение первого условия.

Углы ∠BNM и ∠BСА являются соответственными углами при прямых АС и MN и секущей ВС.

• Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Первое условие выполняется.

Следовательно MN - средняя линия треугольника АВС.