Предмет: Геометрия,
автор: dashagolovacheva99
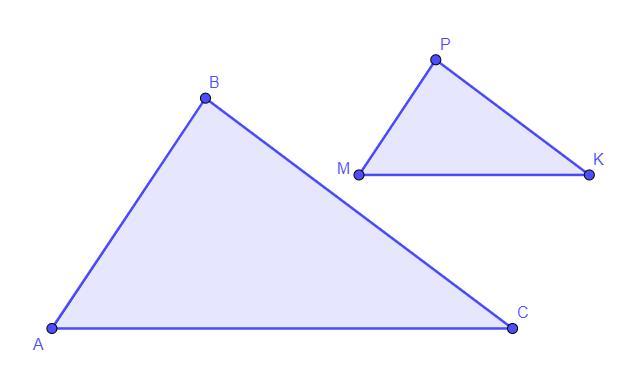
Треугольники АВС и МРК подобны. Стороны АВ, ВС и АС соответственно равны 21 см, 18 см и 15 см. Сторона МК равна 5 см. Найдите периметр треугольника МРК (в см). Единицы измерения в ответе не писать
Ответы
Автор ответа:
3
Ответ:
PΔМРК = 18 см
Объяснение:
Дано: , AB = 21 см, BC = 18 см, AC = 15 см, MK = 5 см
Найти: PΔМРК - ?
Решение: Так как по условию треугольник , то по свойствам подобных треугольников их коэффициент подобия
равен
. По определению периметра треугольника:
PΔABC = AB + BC + AC = 21 + 18 + 15 = 54 см. По свойствам подобных треугольников их периметры соотносятся как коэффициенты подобия, тогда так как , то
см.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: rotanins
Предмет: Английский язык,
автор: peleshko98
Предмет: Русский язык,
автор: freea
Предмет: Алгебра,
автор: zainabkurbanova