Предмет: Математика,
автор: bielovaliza19032002
Пользуясь правилами дифференцирования, найти производные и дифференциалы следующих функций:
Приложения:
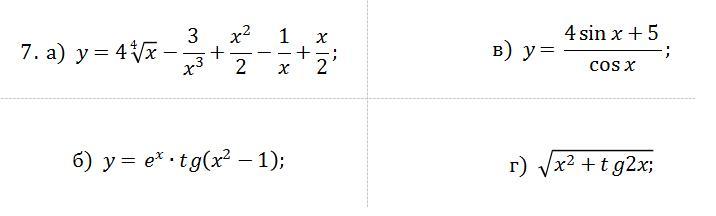
Ответы
Автор ответа:
2
Ответ:
а)
б)
в)
г)
Похожие вопросы
Предмет: Математика,
автор: tadzh038
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: niuyton
Предмет: Математика,
автор: styona2006
Предмет: Математика,
автор: геллі