Question

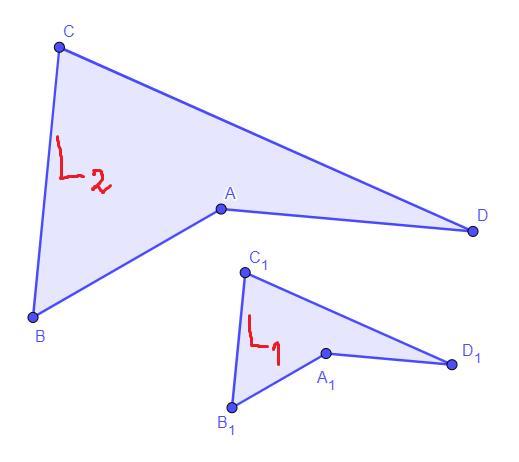
6. Периметр одного из двух подобных многоугольников на 12 см меньше периметра второго многоугольника. Длины больших сторон этих многоугольников 8 см и 12 см. Найди их периметры. Ответы запиши в порядке возрастания.
(Нужно полное решение)​

Answer 1

Ответ:

$P_{1} = 24$ см

$P_{2}= 36$ см

Объяснение:

Дано: $P_{2} = P_{1} + 12$, $L_{2} = 12$ см, $L_{1} = 8$ см

Найти: $P_{1}, P_{2}$ - ?

Решение: Отношение периметров подобных многоугольников по теореме равно отношению длин сторон подобных многоугольников. Тогда: $\dfrac{P_{2}}{P_{1}} = \dfrac{L_{2}}{L_{1}} \Longleftrightarrow P_{2}L_{1} = P_{1}L_{2}$

$(P_{1} + 12)L_{1} = P_{1}L_{2}$

$8(P_{1} + 12)= 12P_{1}$

$8P_{1} + 96 = 12P_{1}$

$96 = 4P_{1}|:4$

$P_{1} = 24$ см.

$P_{2} = P_{1} + 12 = 24 + 12 = 36$ см.