Question

пожалуйста ппомогите быстрее пж надооо

Answer 1

Ответ:

$\displaystyle a-b+c-d=\frac{2}{3} .$

Пошаговое объяснение:

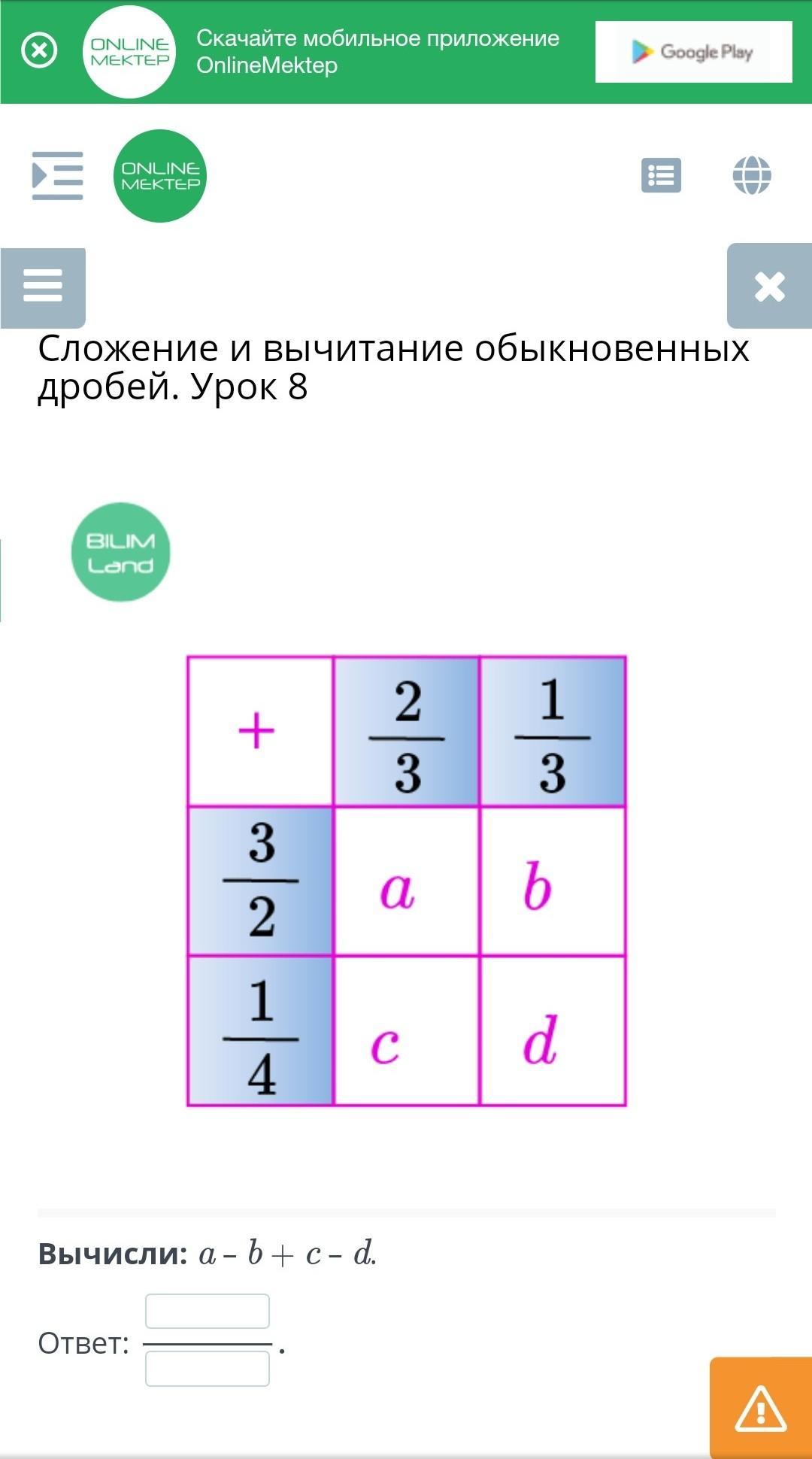
Каждое из значений переменных равно сумме дробей в соответствии с заданной таблицей.

$\displaystyle a = \frac{3}{2} +\frac{2}{3} ; \; \; \; b = \frac{3}{2} +\frac{1}{3} ; \; \; \; c = \frac{1}{4} +\frac{2}{3} ; \; \; \; d = \frac{1}{4} +\frac{1}{3}.$

Требуется найти значение выражения

$\displaystyle a-b+c-d.$

Составим выражение, раскроем скобки с учетом знаков перед скобками,  сгруппируем слагаемые с равными знаменателями, вычислим его значение.

$\displaystyle a-b+c-d=\\\\= \left(\frac{3}{2} +\frac{2}{3}\right)- \left(\frac{3}{2} +\frac{1}{3}\right)+\left(\frac{1}{4} +\frac{2}{3}\right)-\left(\frac{1}{4} +\frac{1}{3}\right)=\\\\=\frac{3}{2} +\frac{2}{3}- \frac{3}{2} -\frac{1}{3}+\frac{1}{4} +\frac{2}{3}-\frac{1}{4} -\frac{1}{3}=\\\\= \left( \frac{3}{2}-\frac{3}{2} \right)+ \left( \frac{2}{3}-\frac{1}{3} +\frac{2}{3}-\frac{1}{3} \right)+ \left( \frac{1}{4}-\frac{1}{4} \right)=\\\\=0+\left(\frac{4}{3} -\frac{2}{3}\right) +0=\frac{2}{3} .$