Предмет: Алгебра,
автор: El86
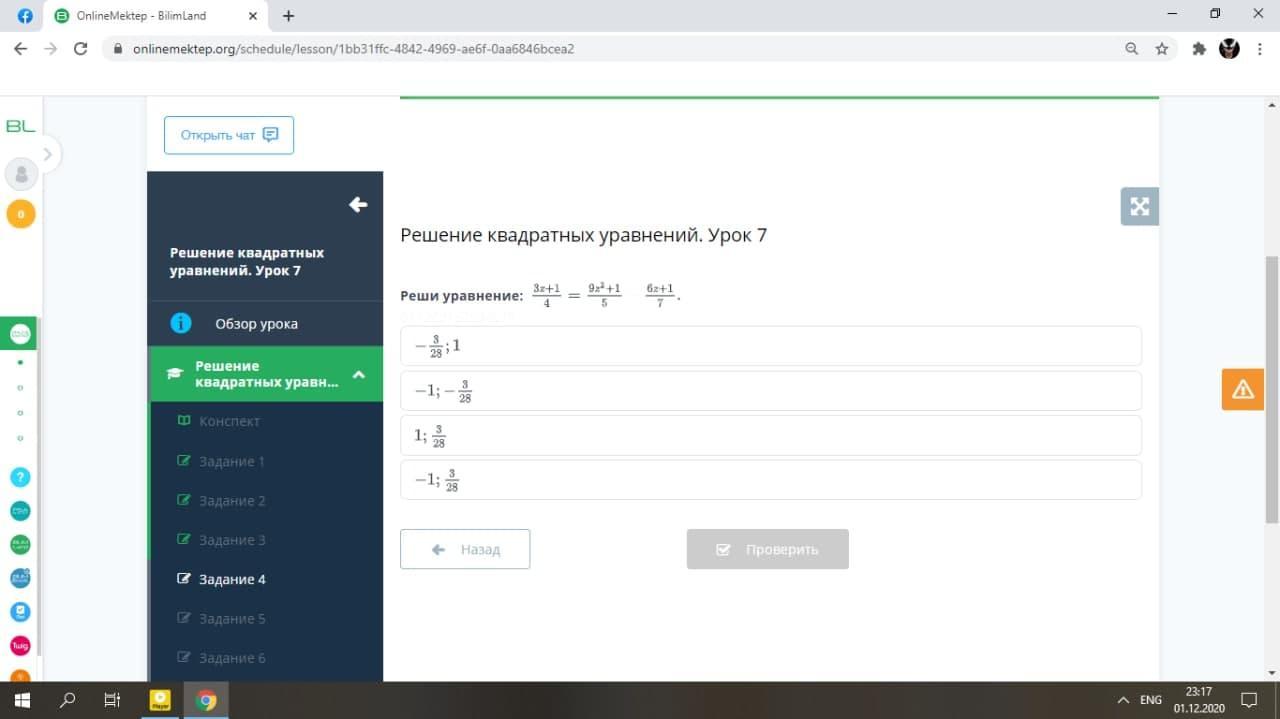
Решение квадратных уравнений. Урок 7
Приложения:
morzh54:
братан по братски какие ответы в начале и в конце, пойми
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
В задании пропущен знак между дробями в правой части, там должен стоять минус:
Сперва приведем все дроби к общему знаменателю 140. Для этого нужно первую дробь умножить на дополнительный множитель 35, вторую — на 28, третью — на 20:
В правой части применим правило вычитания дробей с общим знаменателями: от числителя первой дроби нужно отнять числитель второй, а знаменатель оставить тем же.
У дробей с равными знаменателями числители также будут равны, поэтому:
Раскроем скобки:
Это квадратное уравнение, поэтому перенесем все члены с правой части в левую, сменив при этом их знаки:
Приведем подобные слагаемые:
Разделим обе части уравнения на 9:
Формула дискриминанта:
Найдем корни уравнения:
Похожие вопросы
Предмет: Биология,
автор: vestikmax
Предмет: Химия,
автор: nastya1991997
Предмет: Русский язык,
автор: merzlikinaJ
Предмет: Математика,
автор: stas284
Предмет: Математика,
автор: aslanovramil123