Помогите пожалуйста
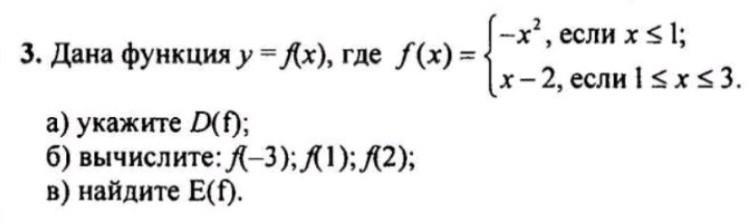
Ответы
Ответ:
а) D(f)=(-∞; 3], или x ∈ (-∞; 3];
б) -9, -1, 0;
в) E(f)=(-∞; 1], или y ∈ (-∞; 1];
Объяснение:
а) D(f) - область определения функции (то, сколько значений X присутствует). Значения даны в условии: , при объединении этих неравенств
, т.е. x ∈ (-∞; 3]
б)
в) E(y) - область определения функции (то, сколько значений Y присутствует). Анализируем данные функции.
y=-x^2 - квадратичная функция, график парабола, ветви вниз и вершина находится в точке (0; 0) - т. начала координат. Т.е., если парабола определена на отрезке , то слева (в отрицательных значениях X) парабола уходит в бесконечность, а справа заканчивается на значении 1. При этом, значение Y 11, т.к. y(1)=-(1)^2=-1.
Т.е. парабола заканчивается в точке (1; -1).
y=x-2 - линейная функция, график прямая. Если подставить значения крайней точки параболы в это уравнение, то окажется, что точка принадлежит прямой. Отсюда можно понять, что раз уж прямая находится на отрезке x ∈ (1; 3), то прямая - продолжает график функции от точки конца параболы. Отсюда учтем, что прямая является отрезком (т.к. ограничена), а значит конец всего графика находится в крайней точке этого отрезка (т.к. функция возрастает на всех значениях X). y(3)=1, т.е. (3; 1) - точка конца отрезка и всего графика. Точка выше вершины параболы, а значит область определения заканчивается на ней.
Ответ:
смотри ниже по каждому пункту
Решение:
а) (Это надо указать ОДЗ Область допустимых значений функции
и она определена значениями заданными в фигурной скобке)
D(f): х∈ (-∞;1] ∪[1;3]
б) f(-3) ( при х= -3 f(x)= -x²)
f(-3)= - (-3)²= -9
при х=1 функция принимает
f(1)=-(-1)²=-1 ( илиf(1)=1-2=-1 )
при х= 2
f(2)=2-2=0
в)Е(f)-Область значений функции
Для нахождения множества значений функции сначала находят множество значений аргумента, затем, используя свойства неравенств, отыскивают соответствующие наименьше и наибольшее значения функции функции.
Е(f) найдем значение функции в максимальной точке при х=3
f(3)=3-2=1
теперь возьмём какую-нибудь дальнюю точку( чтобы понять что там у нас в бесконечности по х и по у происходит) например х=-100
f(-100)= -(-100)²= - 10000 ( чем меньше х - тем меньше у)
Значит Е(f): y ∈ (-∞;1]