Question

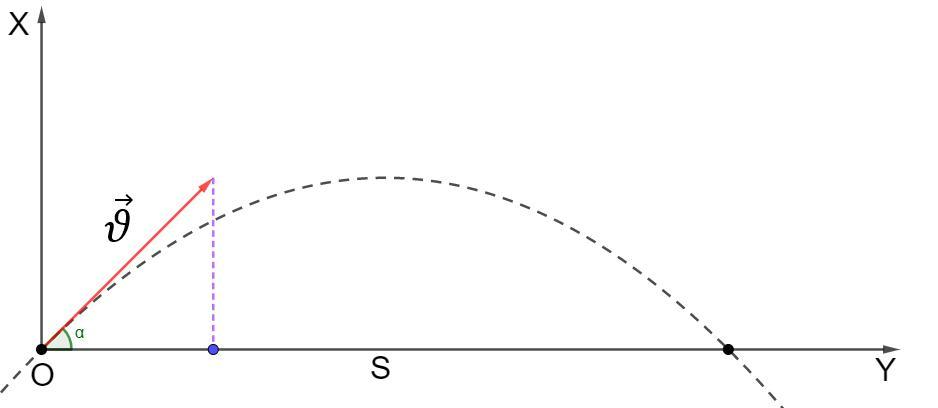
Тело брошено со скоростью 6 м/с с горизонтального участка поверхности Земли. Спустя 0,6 с его скорость оказалась равна начальной по величине. Найдите дальность полёта тела. Ответ запишите в метрах, округлив до сотых. Сопротивлением воздуха пренебречь, ускорение свободного падения считать равным 10 м/с2.

Answer 1

Ответ:

S = 3,12 м

Объяснение:

Дано:

$v_{0} = 6$ м/с

t = 0,6 с

g =  10 м/с²

Найти:

S - ?

----------------------------

Решение:

По формулам дальности полета тела под углом к горизонту составим систему уравнений:

$\displaystyle \left \{ {{S = v_{0}t \cos \alpha } \atop {S = \dfrac{v_{0}^{2}\sin 2\alpha }{g} }} \right \Longrightarrow v_{0}t \cos \alpha = \dfrac{v_{0}^{2}\sin 2\alpha }{g} }$

$v_{0}t \cos \alpha = \dfrac{v_{0}^{2}\sin 2\alpha }{g} }|*g$

$gv_{0}t \cos \alpha = v_{0}^{2}\cdot 2 \sin\alpha \cos \alpha |:(\cos (\alpha) \cdot v_{0})$

$gt = 2v_{0} \sin \alpha \Longrightarrow \sin \alpha = \dfrac{gt}{2v_{0}}$

$\sin\alpha =$ 10 м/с² * 0,6 с / 2 * 6 м/с = 0,5 ⇒ α = 30°

$S = v_{0}t \cos \alpha$

$S =$ 10 м/с² * 0,36 с² * √3 / 2 = 1,8√3 ≈ 3,12 м

Ответ: S = 3,12 м.