Предмет: Алгебра,
автор: omegenila
алгебра уравнения срочно
Приложения:
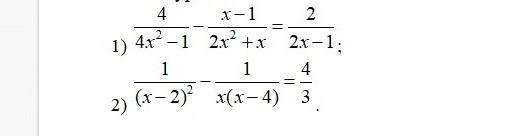
Ответы
Автор ответа:
1
Ответ:
Объяснение:
ОДЗ:
Решение:
Корень х₁ не удовлетворяет ОДЗ.
ОДЗ:
Решение:
Делители цифры 3:
Подставим вместо "х" единицу:
Единица обращает уравнение в верное равенство ⇒ один из множителей равен (х – 1). Разделим исходный многочлен на (х – 1):
Делители числа –3:
Подставим вместо "х" единицу:
Единица не обращает уравнение в верное равенство.
Подставим вместо "х" тройку:
Цифра 3 обращает уравнение в верное равенство ⇒ один из множителей равен (х – 3). Разделим исходный многочлен на (х – 3):
Мы нашли корни последнего уравнения. Два других корня мы отыскали, когда подбирали число для разложения выражения на множители.
Найденные корни удовлетворяют ОДЗ.
Похожие вопросы
Предмет: Другие предметы,
автор: ghoust14
Предмет: Математика,
автор: olegskorr1
Предмет: Другие предметы,
автор: MalikaSal
Предмет: История,
автор: leria11111111111
Предмет: Алгебра,
автор: HIpsTER22