Предмет: Геометрия,
автор: linevaannanik
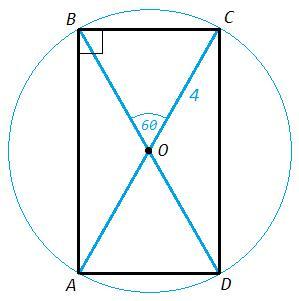
В окружности диаметры АС и ВD пересекаются под углом 60 . Определите вид четырёхугольника АВСD и найдите его периметр ,если радиус окружности равен 4 см.
Ответы
Автор ответа:
2
OA=OB=OC=OD (радиусы)
Диагонали четырехугольника точкой пересечения делятся пополам - признак параллелограмма.
Диагонали параллелограмма равны - признак прямоугольника.
ABCD - прямоугольник.
В сантиметрах
BOC - равнобедренный с углом 60° => равносторонний
BC=OC =4, AC=OA+OC =8
AB =√(AC^2 -BC^2) =4√3 (т. Пифагора)
P(ABCD) =2(AB+BC) =8√3 +8 (см)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: reginka5551
Предмет: Математика,
автор: Ангелочек227
Предмет: Математика,
автор: kopyllera
Предмет: Математика,
автор: andreynaumov90
Предмет: География,
автор: Milana000000111