Question

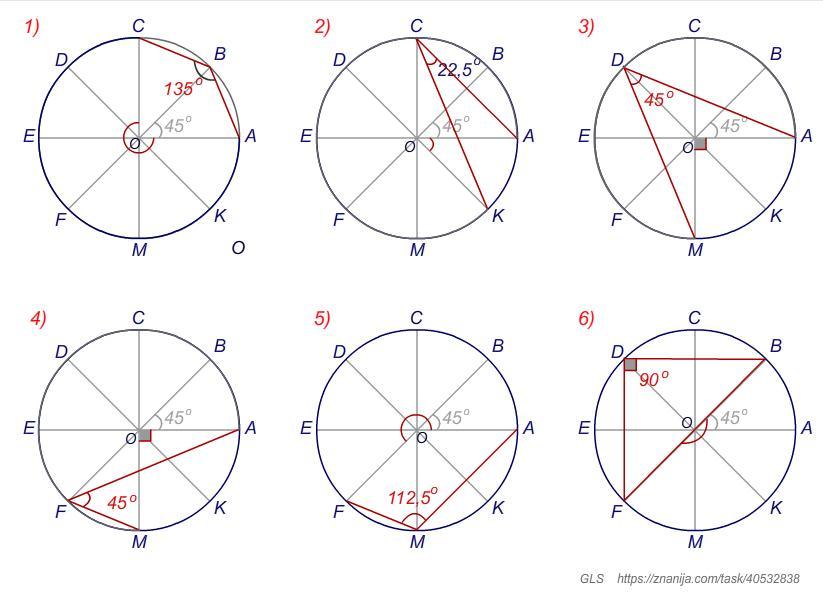
Точки A, B, C, D, E, F, М и К разделили окружность на 8 равных дуг. Найди градусные меры указанных углов.
ABC =
ACK=
ADM=
AFM=
AMF=
BDF=

Answer 1

Ответ:

∠ABC = 135°;   ∠ACK = 22,5°;   ∠ADM = 45°;  ∠AFM = 45°; ∠AMF = 112,5°; ∠BDF = 90°.

Объяснение:

Точки A, B, C, D, E, F, М и К разделили окружность на 8 равных дуг.

Градусная мера каждой дуги:

$\displaystyle \frac{360}{8} =45^{o}$

На каждую дугу опирается центральный угол, градусная мера которого равна градусной мере дуги и равна 45°.

• Для нахождения величин углов воспользуемся теоремой: вписанный угол равен половине соответствующего центрального угла.
• Вписанный и центральный углы являются соответствующими, если они опираются на одну и ту же дугу.

1) Вписанному углу ABC соответствует центральный угол COA, который опирается на дугу AKMFEDC.

$\displaystyle \angle ABC=\frac{45^{o} \cdot 6}{2} =\frac{270^{o}}{2} =135^{o}$

2) Вписанному углу ACK соответствует центральный угол AOK=45°, который опирается на дугу AK.

$\displaystyle \angle ACK=\frac{45^{o}}{2} =22,5^{o}$

3) Вписанному углу ADM соответствует центральный угол ADM=90°, который опирается на дугу AKM.

$\displaystyle \angle ADM=\frac{90^{o}}{2} =45^{o}$

4) Вписанному углу AFM соответствует центральный угол AOM = 90°, который опирается на дугу FMK.

$\displaystyle \angle AFM=\frac{90^{o}}{2} =45^{o}$

5) Вписанному углу AMF соответствует центральный угол AOF, который опирается на дугу ABCDEF.

$\displaystyle \angle AMF=\frac{45^{o} \cdot 5}{2} =\frac{225^{o}}{2} =112,5^{o}$

6) Вписанный угол BDF опирается на диаметр BF, значит он прямой.

∠BDF = 90°.