Предмет: Алгебра,
автор: komaksyt
Помогите решить, отдаю все баллы
Приложения:
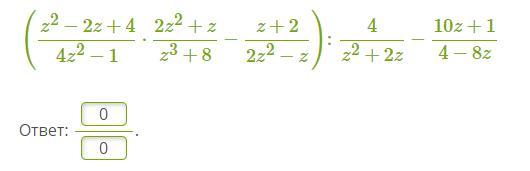
komaksyt:
але
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Nести
Предмет: Биология,
автор: ody
Предмет: Информатика,
автор: aliyaabdulova
Предмет: Математика,
автор: angelina2005hs
Предмет: Биология,
автор: Евгений1234949