Предмет: Алгебра,
автор: finogenovaa2410
помогите срочно нужно
Приложения:
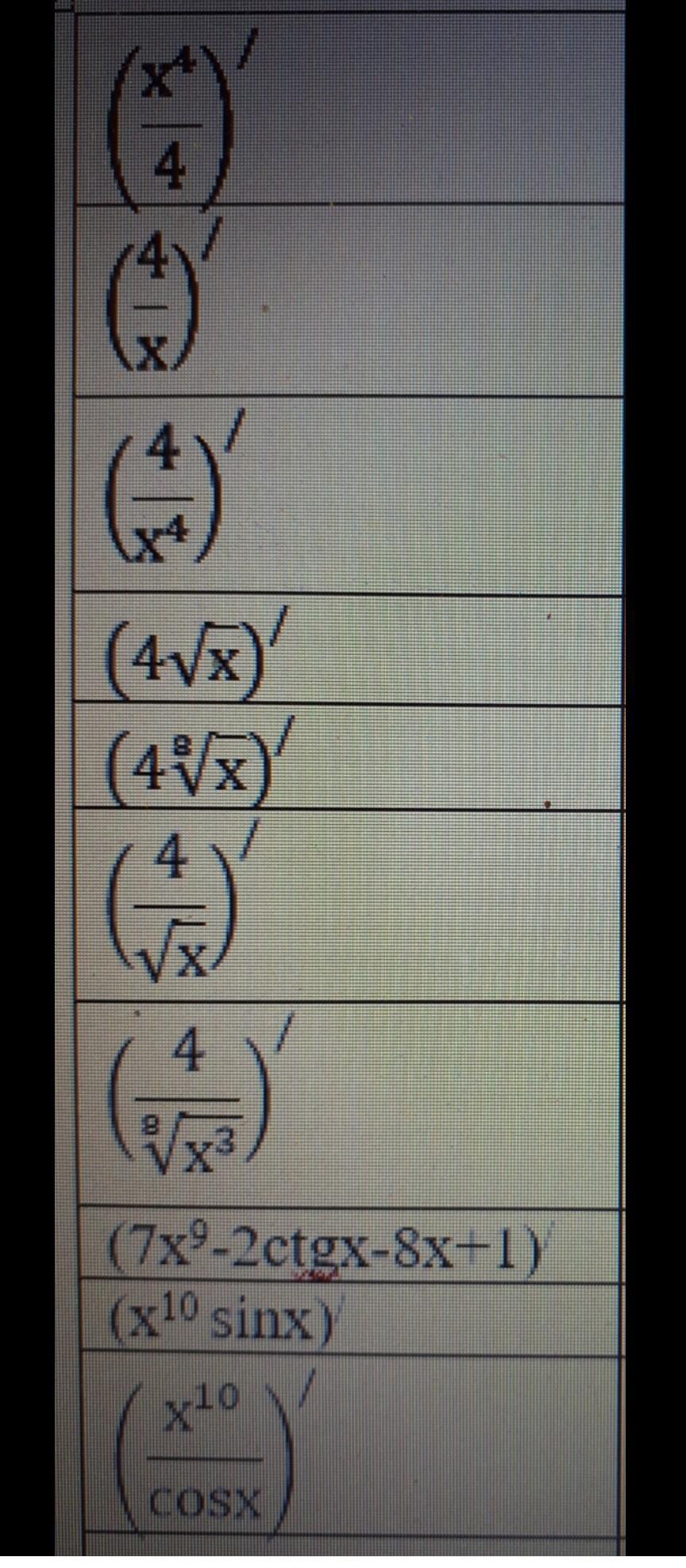
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: Волика666
Предмет: Русский язык,
автор: Alioshaaliabiev
Предмет: Математика,
автор: zhupanovfil
Предмет: Математика,
автор: Денис20051142
Предмет: Биология,
автор: аааааа98