Предмет: Математика,
автор: n28m20061
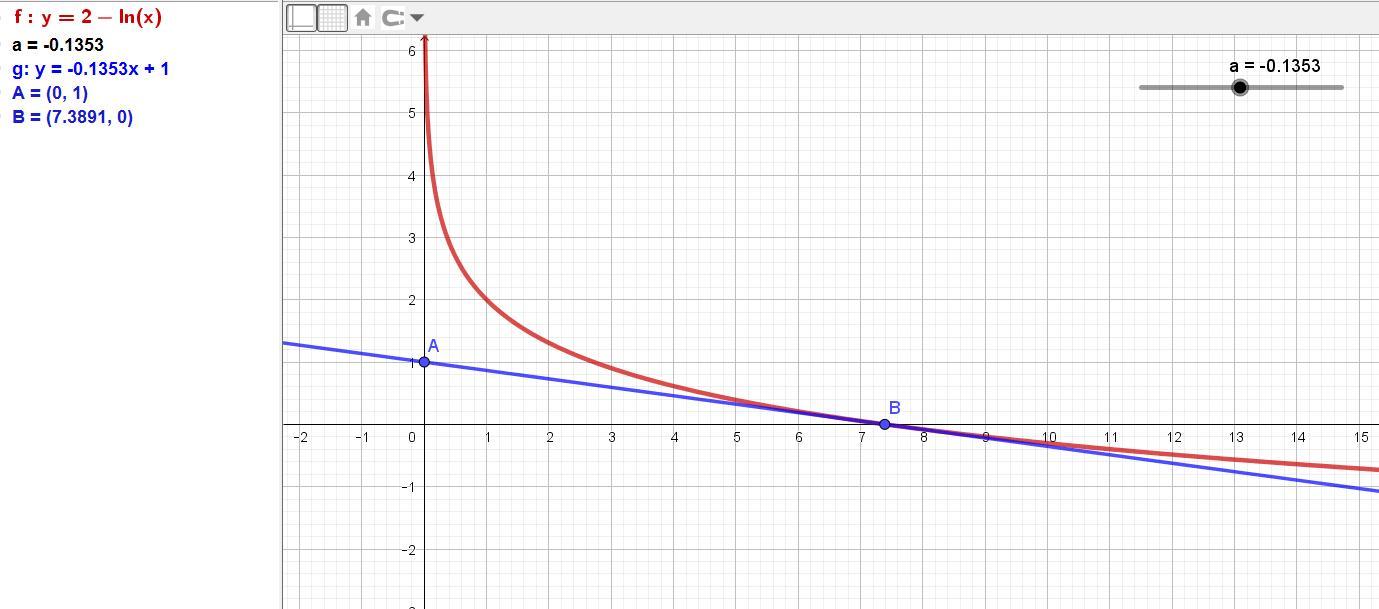
При каком значении параметра a прямая y=ax+1 является касательной к графику функции y=2-lnx
Ответы
Автор ответа:
1
Угловой коэффициент касательной к графику функции равен производной функции в точке касания.
Производная функции y=2-lnx равна -1/x.
Значит, уравнение касательной имеет вид y = (-1/x)*x+ 1 или y = 0.
В точке касания координаты кривой и прямой равны.
Приравняем: 2 - lnx = 0, отсюда x = e².
Точка касания В = (e²; 0).
Известна точка прямой на оси Оу - это свободный член уравнения прямой, то есть у = 1 при х = 0.
По двум точкам находим угловой коэффициент касательной.
k = Δy/Δx = (0 - 1)/(e² - 0) = -1/e².
Ответ: а = -1/e².
Приложения:
Похожие вопросы
Предмет: Литература,
автор: maska3
Предмет: Математика,
автор: valeriamai81
Предмет: Литература,
автор: urkinbaeva
Предмет: Математика,
автор: guast1
Предмет: Литература,
автор: катя4794