Предмет: Алгебра,
автор: reyofer251
Найти tg d даю 25 баллов
Приложения:

Ответы
Автор ответа:
0
Ответ:
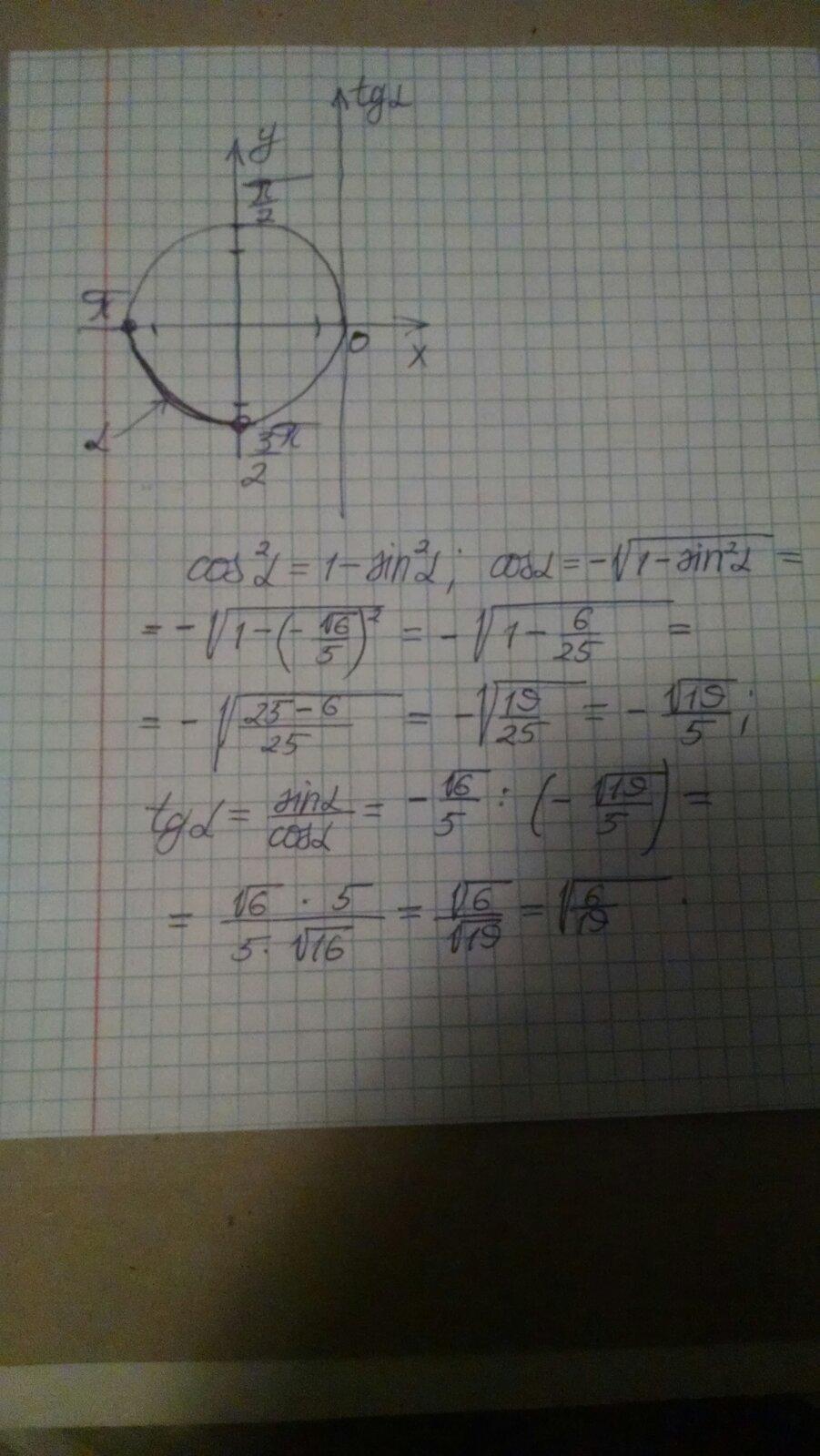
угол находится в третьей четверти => cosa отрицательный
Автор ответа:
0
Ответ: tgα=√(6/19).
Объяснение:
Приложения:
Похожие вопросы