Предмет: Алгебра,
автор: hehsjsjs
распишите подробно решение неравенства, спасибо
Приложения:
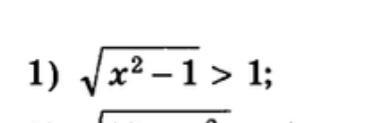
Ответы
Автор ответа:
2
Ответ:
ОДЗ:
х принадлежит (-беск;-1]U[1;+беск).
Возведем обе части во 2 степень:
х принадлежит
Пересекаем с ОДЗ и получаем ответ:
х принадлежит
Похожие вопросы
Предмет: Биология,
автор: ПЕРВОООЕСЕНТЯБРЯ
Предмет: Физика,
автор: biostar2002
Предмет: Математика,
автор: Танюшка1309
Предмет: Литература,
автор: Vika23112004
Предмет: Литература,
автор: донияр1