Предмет: Алгебра,
автор: ata221
30 баллов. Знатоки алгебры, помогите, пожалуйста, решить уравнение.

Ответы
Автор ответа:
2
ata221:
спасибо!!!
Автор ответа:
1
Ответ:
x(1)=-pi/24+pin ; n€Z
x(2)=5/24pi+pin ; n€Z.
Приложения:
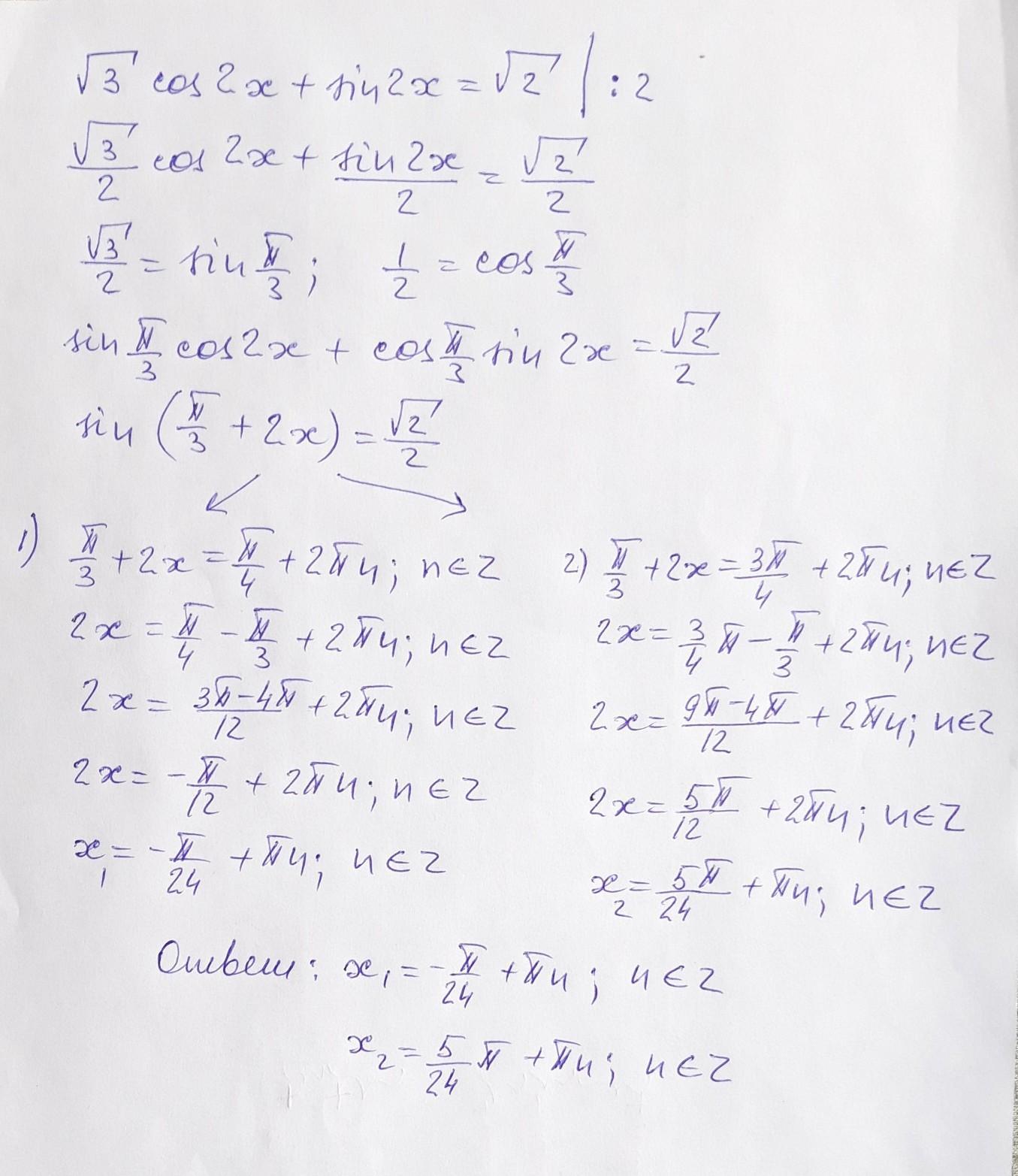
Похожие вопросы
Предмет: Математика,
автор: ladyparasyuk
Предмет: Английский язык,
автор: dik2014
Предмет: Математика,
автор: miyka13
Предмет: Геометрия,
автор: Darya10030499