11.11
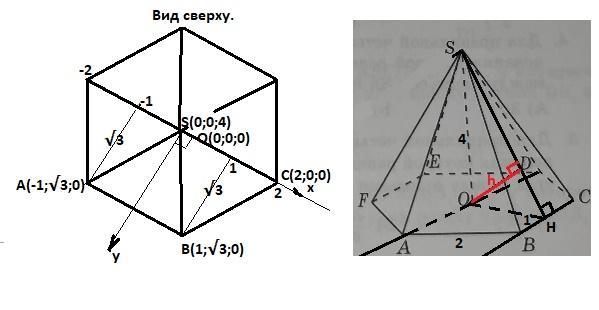
В правильной шестиугольной пирамиде SABCDEF стороны основания равны 2 см , высота 4 см . Найдите расстояние от точки А до плоскости SBC
(расстояние находить по формуле и путем введения координатной системы ...)
Ответы
Ответ:
Расстояние равно (4√57)/19 см.
Объяснение:
В правильной шестиугольной пирамиде SABCDEF стороны основания равны 2 см , высота 4 см . Найдите расстояние от точки А до плоскости SBC.
1. Координатный метод.
Привяжем систему координат к пирамиде так, что ось 0Z совпадет с высотой пирамиды SO, а ось 0Х - пройдет по диагонали FC. Тогда ось 0Y пойдет по высоте правильного треугольника АОВ и имеем точки:
A(-1;√3;0). S(0;0;4). C(2;0;0) и В(1;√3;0).
Уравнение плоскости SBC найдем по формуле:
|x-x1 x2-x1 x3-x1 |
|y-y1 y2-x1 y3-x1 | = 0.
|z-z1 z2-x1 z3-x1 |
Тогда, подставив координаты точек, получим определитель:
|x-0 2 1 |
|y-0 0 √3 | = 0. => x·| 0 √3 | - y·| 2 1 | + (z-4)·| 2 1 | = 0.
|z-4 -4 -4 | |-4 -4 | |-4 -4 | | 0 √3 |
(4√3)·x + 4y + 2√3·z - 8√3 = 0. - Уравнение с коэффициентами
А = 4√3, В = 4, С = 2√3 и D = -8√3.
Расстояние между точкой M(x;y;z) и плоскостью, заданной уравнением
Аx+By+Cz+D=0 находится по формуле:
d = |A·Mx+B·My+C·Mz+D|/(√(A²+B²+C²)). В нашем случае:
d = |-4√3+4√3+0-8√3|/(√(48+16+12)) = 8√3/√76 = (4√57)/19.
Геометрический метод.
Учитывая, что сторона основания ВС параллельна диагонали AD правильного шестиугольника, можем сказать, что расстояние между точкой А и плоскостью SBC равно расстоянию от точки О до этой плоскости.
Это расстояние - перпендикуляр из прямого угла треугольника SOH, где ОН - высота правильного треугольника ВОС, а SH - апофема боковой грани.
ОН = √3 (по формуле). SH = √(SO²+OH²) = √(16+3) = √19.
Высота из прямого угла равна h = a·b/c = 4·√3/√19 = (4√57)/19.