Предмет: Алгебра,
автор: pashagutorov00
Найти производную третьего порядка.
Приложения:
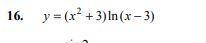
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Надо разделить эту производную на 3 отдельных производных
---------------------------------------
---------------------------------------
Я не смог здесь подробно объяснить т.к выражение было слишком большое
Похожие вопросы
Предмет: Математика,
автор: dfgtu71
Предмет: Другие предметы,
автор: tyuooeftyu2013
Предмет: Русский язык,
автор: yiya
Предмет: Математика,
автор: Julia1192938474
Предмет: Математика,
автор: danchikyuninozespo