Предмет: Математика,
автор: 556789100niks
Найти производную y′ .
Приложения:
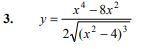
Ответы
Автор ответа:
0
Ответ:
Находим по формуле:
Похожие вопросы
Предмет: Русский язык,
автор: pinkamenapie27
Предмет: Английский язык,
автор: TemkaVoprosist
Предмет: Математика,
автор: AAllii
Предмет: Математика,
автор: Айсара10