Предмет: Математика,
автор: valeriamakinina2
Помогите решить систему уравнения
Приложения:
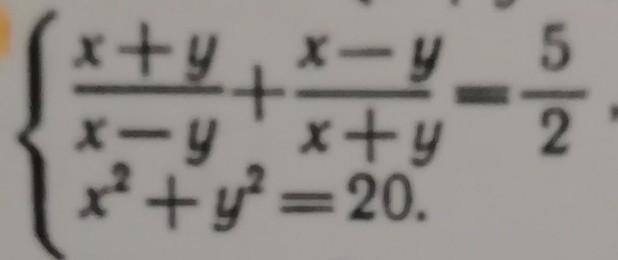
Ответы
Автор ответа:
2
Ответ: х=3√2 ; у=√2.
Пошаговое объяснение:
Приведем (1) уравнение к общему знаменателю,сократим, приведем подобные , получим систему такого вида:
-х²+9у=0
х²+у²=20
Сложим уравнения.
10у²=20
у²=2.
у=√2.
Найдем х:
х²=20-у²=20-2=18.
х=√18=3√2
Аноним:
хотела добавить: х=(+)(-) 3 корень из2 ; так же у=(+)(-) корень из2..
Автор ответа:
1
Ответ:
Пошаговое объяснение:
==>
==>
==>
==>
==>
==>
==>
==>
==>
==>
==>
Похожие вопросы
Предмет: Русский язык,
автор: GHT1
Предмет: Алгебра,
автор: lenakorpa4eva
Предмет: Математика,
автор: Staroverova2004
Предмет: Математика,
автор: абдул211
Предмет: История,
автор: filan905Nastyaph