Предмет: Алгебра,
автор: 3060XLXO
СРОЧНО!!!!!!!!! АЛГЕБРА
Приложения:
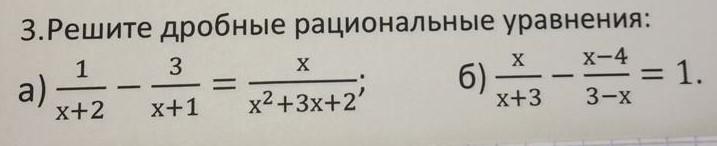
Ответы
Автор ответа:
1
Ответ:
а) x = или
б) x₁ = ; x₂ =
Объяснение:
а)
или
б)
₁
;
₂
Похожие вопросы
Предмет: Математика,
автор: малышка12345678
Предмет: Русский язык,
автор: minaf
Предмет: Математика,
автор: anastasiapisar
Предмет: Литература,
автор: sergeyxo1337
Предмет: Математика,
автор: Pug9922