Предмет: Алгебра,
автор: Zlobinsasha2000five
Пожалуйста, помогите ( Прошу уже 3й раз, никто не помогает(
(Все 6 уравнений)
Приложения:
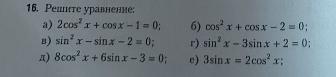
tamarabernukho:
Не более 3 заданий...
Откуда вы это взяли?
Ответы
Автор ответа:
2
Ответ:
замена:
n принадлежит Z.
корень t=2 не подходит , так как значения синуса входят только в [-1;1].
n принадлежит Z.
первый корень не подходит
n принадлежит Z.
второй корень не подходит
n принадлежит Z.
первый корень не подходит
n принадлежит Z.
второй не подходит
n принадлежит Z.
Спасибо огромное))
Похожие вопросы
Предмет: Математика,
автор: gaga2090
Предмет: Математика,
автор: daryakrekova
Предмет: Математика,
автор: mustaev84
Предмет: Математика,
автор: 14sanka
Предмет: Физика,
автор: MC10001