Предмет: Математика,
автор: annaznova91
Пожалуйста, помогите решить интергралы
Приложения:
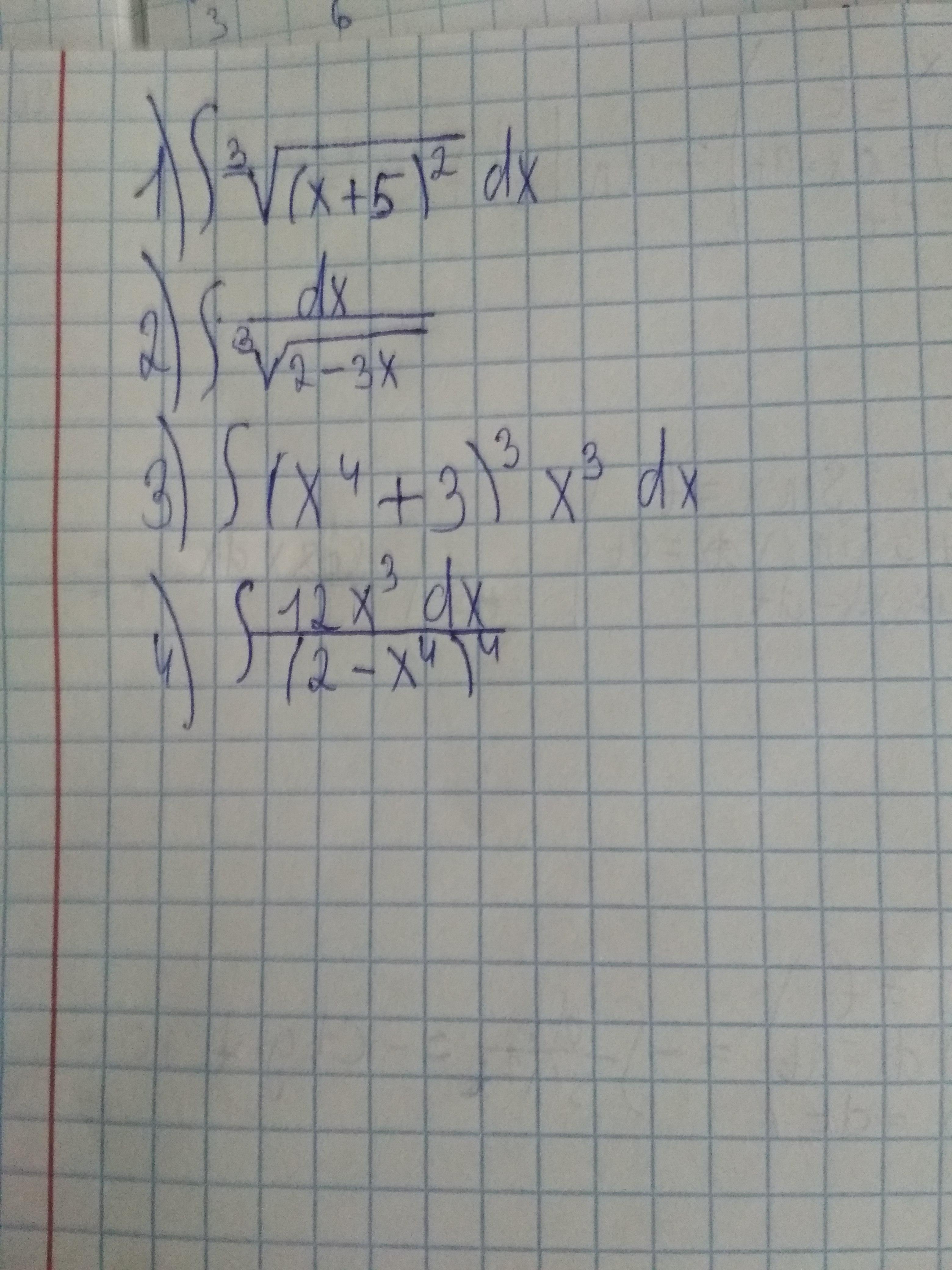
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: 2050904taxmin
Предмет: Математика,
автор: janna14
Предмет: Английский язык,
автор: kirak46
Предмет: Математика,
автор: fedorenkoallaf
Предмет: Математика,
автор: Kamalova8Munira