Предмет: Математика,
автор: gfdgfdfdggfdgdf
Решите пожалуйста полностью)
Приложения:
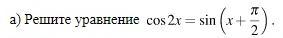
Ответы
Автор ответа:
1
Ответ:
n принадлежит Z.
Похожие вопросы
Предмет: Математика,
автор: nastia20032
Предмет: Русский язык,
автор: NickiAllex
Предмет: Английский язык,
автор: crazycraftfeed
Предмет: Математика,
автор: DvoeglazovaSovushka
Предмет: Химия,
автор: шейда1