Предмет: Алгебра,
автор: NamiSupport
Помогите решить один интеграл, очень срочно! Под номером 15
Отдаю все баллы что есть
Приложения:
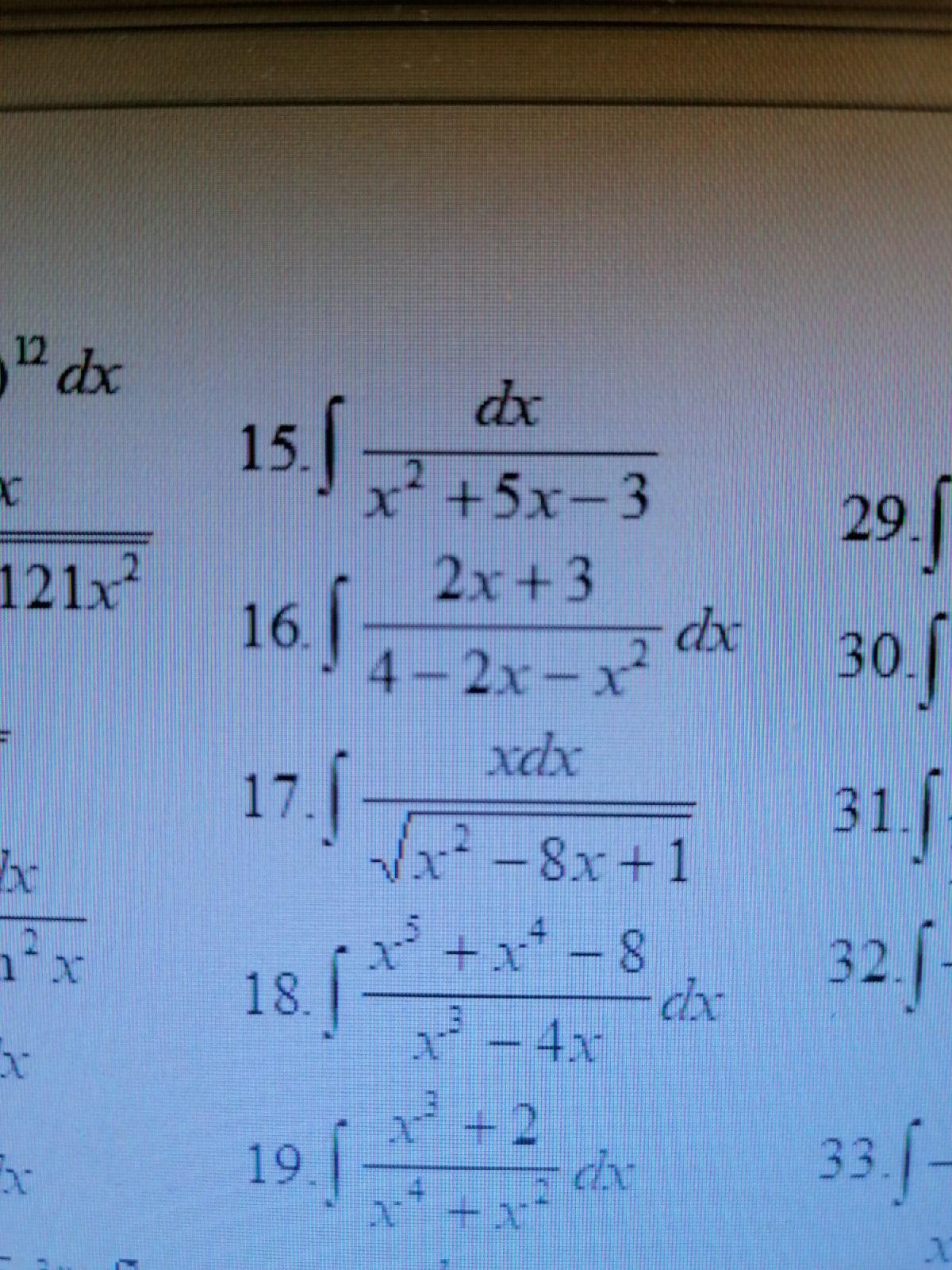
Ответы
Автор ответа:
1
Ответ:
Выделим в знаменателе квадрат суммы:
Когда подставим это в интеграл, можно будет заметить в нем табличный:
Получаем:
NamiSupport:
Спасибо большое)
Похожие вопросы
Предмет: Математика,
автор: nato4ka1708
Предмет: Математика,
автор: asyadalgatova
Предмет: Химия,
автор: Sofiya35
Предмет: Литература,
автор: bruzaegorozm93p
Предмет: ОБЖ,
автор: Илья0956