алгебра 8 класс. Помогите решить пожалуйста.
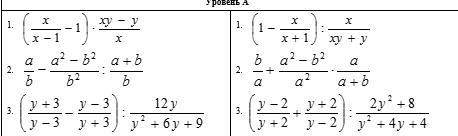
Ответы
сначала я решу первый (левый) столбик
1)(x/x-1 -1)*xy-y/x = x-(x-1)/x-1 * y*(x-1)/x = x-x+1/x-1 * y*(x-1)/x = 1/x-1 * y*(x-1)/x = y/x
2)a/b - a^2-b^2/b^2 : a+b/b = a/b - (a-b)*(a+b)/b^2 * b/a+b = a/b - a-b/b = a-(a-b)/b = a-a+b/b = b/b = 1
3)(y+3/y-3 - y-3/y+3) : 12y/y^2+6y+9 = (y+3)^2-(y-3)^2/(y-3)*(y+3) * y^2+6y+9/12y = 6*2y/(y-3)*(y+3) * (y-3)^2/12y = 12y/y-3 * y+3/12y = 1/y-3 * (y+3) = y+3/y-3
теперь второй (правый) столбик
1)(1- x/x+1) : x/xy+y = x+1-x/x+1 * xy+y/x = 1/x+1 * y*(x+1)/x = y/x
2)b/a + a^2-b^2/a^2 * a/a+b = b/a + (a-b)*(a+b)/a * 1/a+b = b/a + a-b/a = b+a-b/a = a/a = 1
3)(y-2/y+2 - y+2/y-2) : 2y^2+8/y^2+4y+4 = (y-2)^2+(y+2)^2/(y+2)*(y-2) * y^2+4y+4/2y^2+8 = (y-2)^2+(y+2)^2/(y+2)*(y-2) * (y-2)^2/2y^2+8 = (y-2)^2+(y+2)^2/y-2 * y+2/2y^2+8 = ((y-2)^2+(y+2)^2)*(y+2)/(y-2)*(2y^2+8) =
(y^2-4y+4+y^2+4y+4)*(y+2)/(y-2)*(2y^2+8) = (2y^2+8)*(y+2)/(y-2)*(2y^2+8) =
y+2/y-2