Предмет: Геометрия,
автор: Аноним
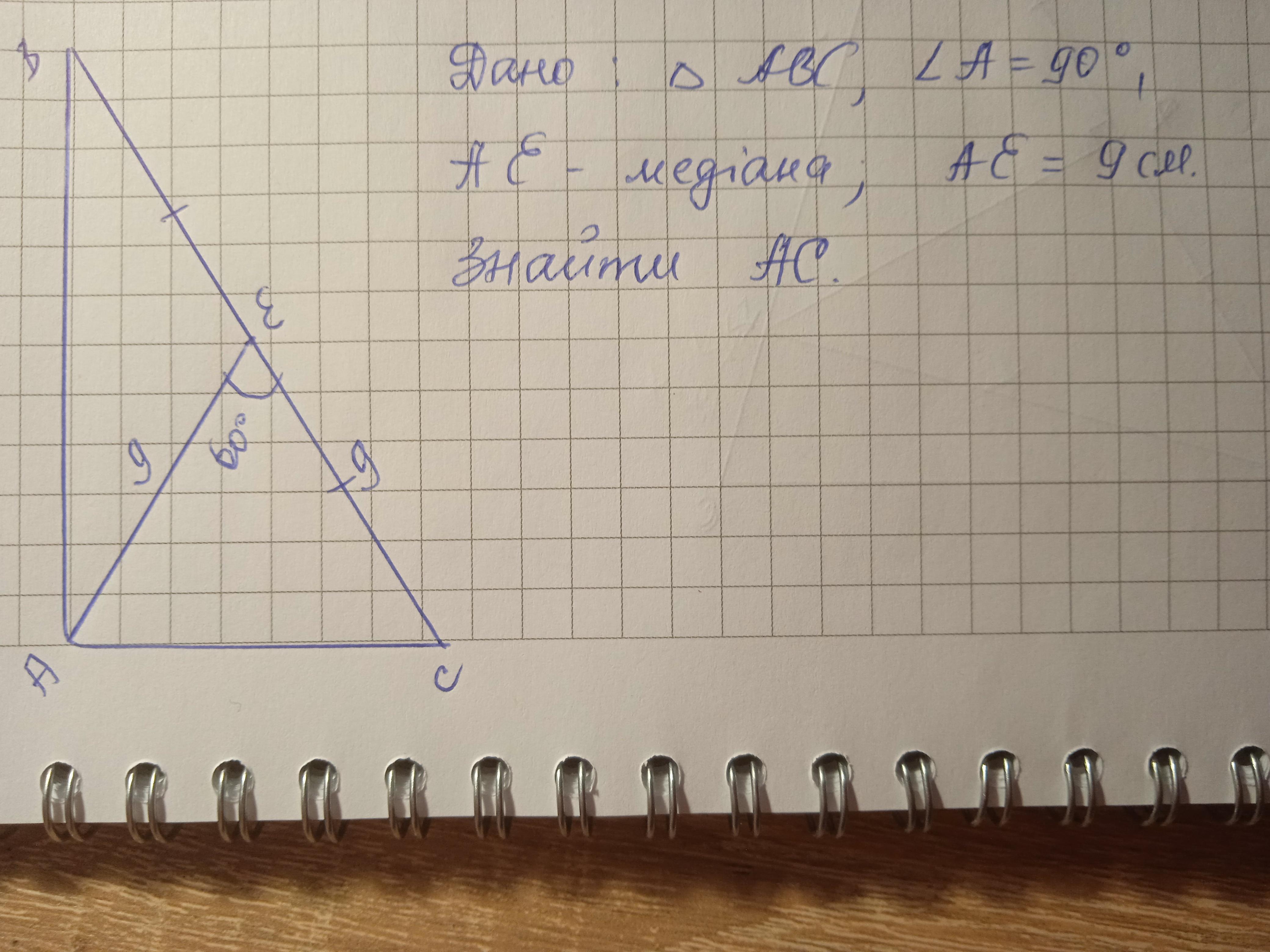
6.Знайдіть менший катет прямокутного трикутника, якщо його медіана
дорівнює 9 см і утворює з гіпотенузою кут 60°.
Ответы
Автор ответа:
2
Ответ:
9 см
Объяснение:
Медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи.
Розглянемо ΔАЕС, СЕ=АЕ=9 см, отже ΔАЕС - рівнобедрений.
∠ЕАС=∠С як кути при основі рівнобедреного трикутника.
∠ЕАС=∠С=(180-60):2=60°
отже, ΔАЕС - рівносторонній, тому АЕ=СЕ=АС=9 см.
Приложения:
Автор ответа:
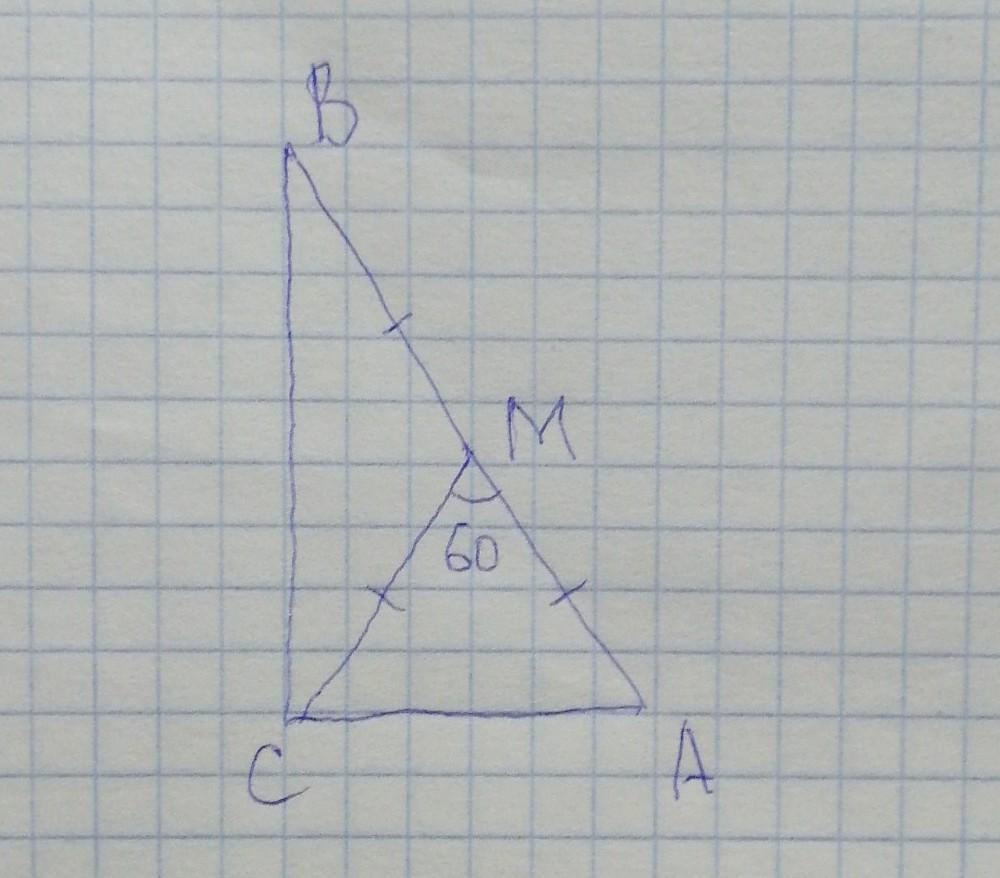
0
Объяснение:
Пусть тр-к АВС < С=90 СМ- медиана
СМ=9 см <СМА=60 градусов
НАЙТИ : меньший катет
В прямоугольном тр-ке медиана равна половине гитотенузы :
СМ=1/2×АВ
СМ=АМ=МВ
Тр-кСМА равнобедренный, т к СМ=АМ
если<СМА=60,значит <АСМ=<МАС=(180-60)/2=
=60 градусов,
тр-к СМА- равносторонний, тогда
АС=СМ=АМ=9 см
<А=60,то <В=90-<А=90-60=30 градусов
В тр-ке против меньшего угла лежит меньшая сторона, значит катет АС меньший и равен 9 см
Приложения:
Похожие вопросы
Предмет: Математика,
автор: zaxra12
Предмет: Английский язык,
автор: Klassnik
Предмет: Английский язык,
автор: olga1997s
Предмет: Химия,
автор: akivoim
Предмет: История,
автор: Serenity01