Question

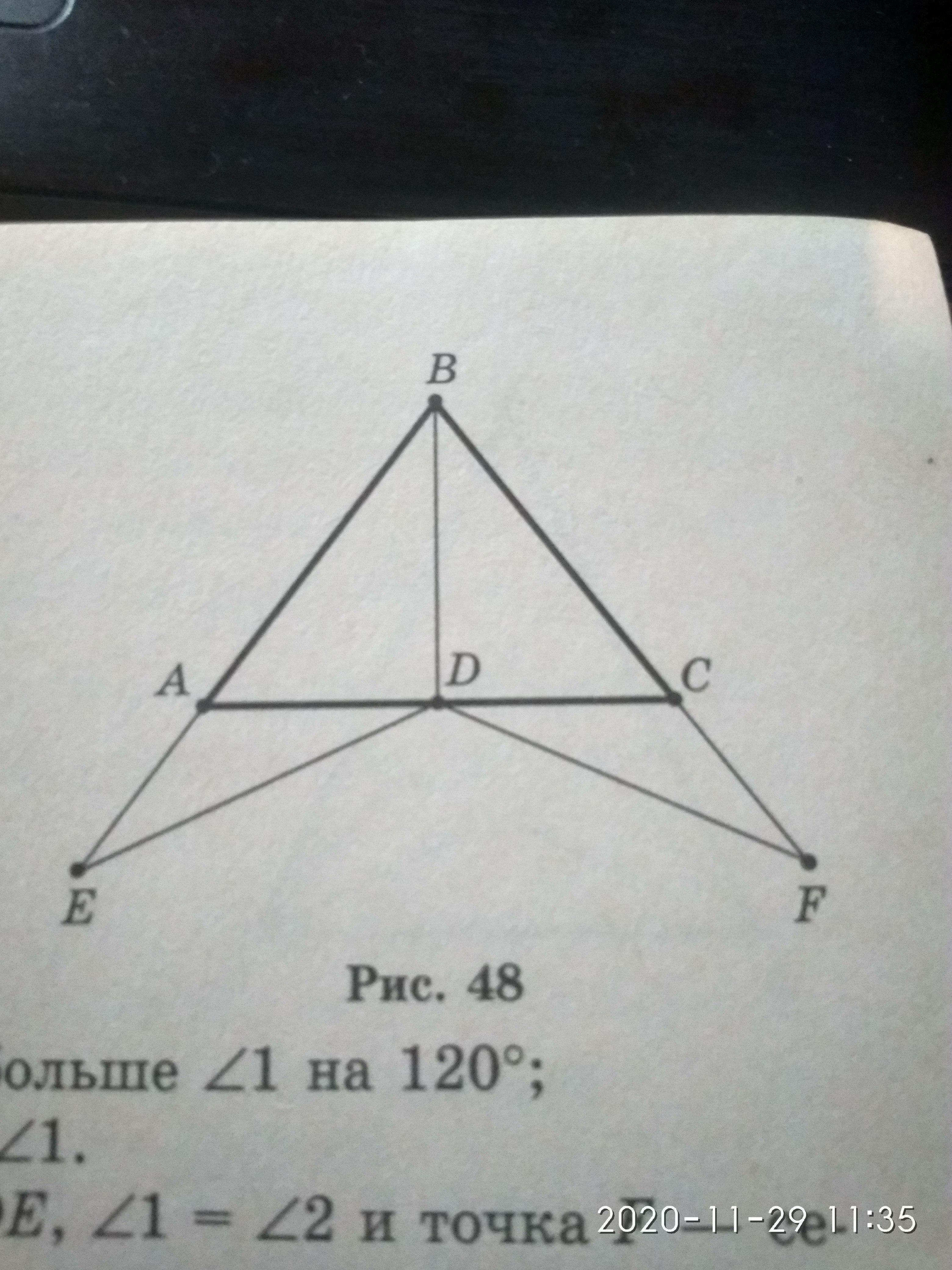
В треугольнике ABC AB=BC, отрезок BD - медиана. На лучах BA и BC (см. Рис.) Взяты соответственно точки E и F такие, что BE =BF. Докажите что:
а) Треугольник ADE= треуг. CDF;
б)треуг. DEF - равнобедренный;
в) треуг. BDE = треуг. BDF

Answer 1

Ответ:

а) треугольник АДЕ и СДФ имеют общую точку Д через них проходит прамая АС.

АД= ДС потому что медиана делит основу треугольника поровно. и БЕ равно БФ

Из этого выплывет, что АДЕ равен СДФ

б) по скольку АДЕ равен СДФ, значит ЕД равна ДФ.

и угол ДЕФ равен углу ДФЕ. Выходит, что треугольник ДЕФ равнобедренный

в) По скольку медиана делит основу треугольника АВС пополам и ВЕ равна ВФ, а АД равна ВС. значит, что треугольник АБД равен треугольнику ДБС. А треугольник АДЕ равен СДФ, выходит что ВДЕ равен ВДФ.

Объяснение:

готово.