Предмет: Геометрия,
автор: evgeniacepurnova61
Найдите площадь треугольника АВС
Приложения:
Ответы
Автор ответа:
7
Дано :
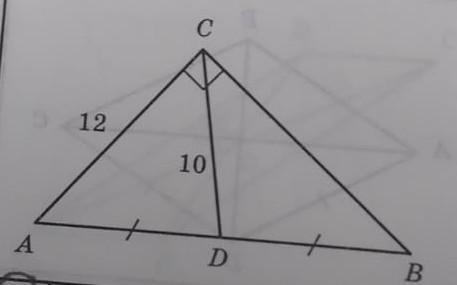
∆АВС — прямоугольный (∠С = 90°).
AD = BD.
АС = 12, CD = 10.
Найти :
S(∆ABC) = ?
Решение :
Так как D — середина АВ, то CD — медиана ∆АВС (по определению).
- В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине.
Следовательно, АВ = 2CD = 2*10 = 20.
По теореме Пифагора найдём длину катета СВ :
AB² = AC² + CB²
CB² = AB² - AC² = 20² - 12² = 400 - 144 = 256 => CB = √CB² = √256 = 16.
- Площадь прямоугольного треугольника равна половине произведения его катетов.
Следовательно, S(∆ABC) = ½*AC*CB = ½*12*16 = 96 (ед²).
Ответ :
96 (ед²).
Похожие вопросы
Предмет: Математика,
автор: vasiliynechaev
Предмет: Английский язык,
автор: rozamsms
Предмет: Русский язык,
автор: 32154nfh
Предмет: Алгебра,
автор: antonotlichnik1
Предмет: Литература,
автор: Qulya11