Предмет: Алгебра,
автор: mddda
ПОМОГИТЕ!!! КТО СДЕЛАЕТ 1,2,4 ДАМ 100 БАЛЛОВ
Приложения:

kayemelyanenko:
тут 50 баллов как ты их накопил
Тут 100 баллов.
Ответы
Автор ответа:
0
Ответ:
решение на фотографии
Приложения:


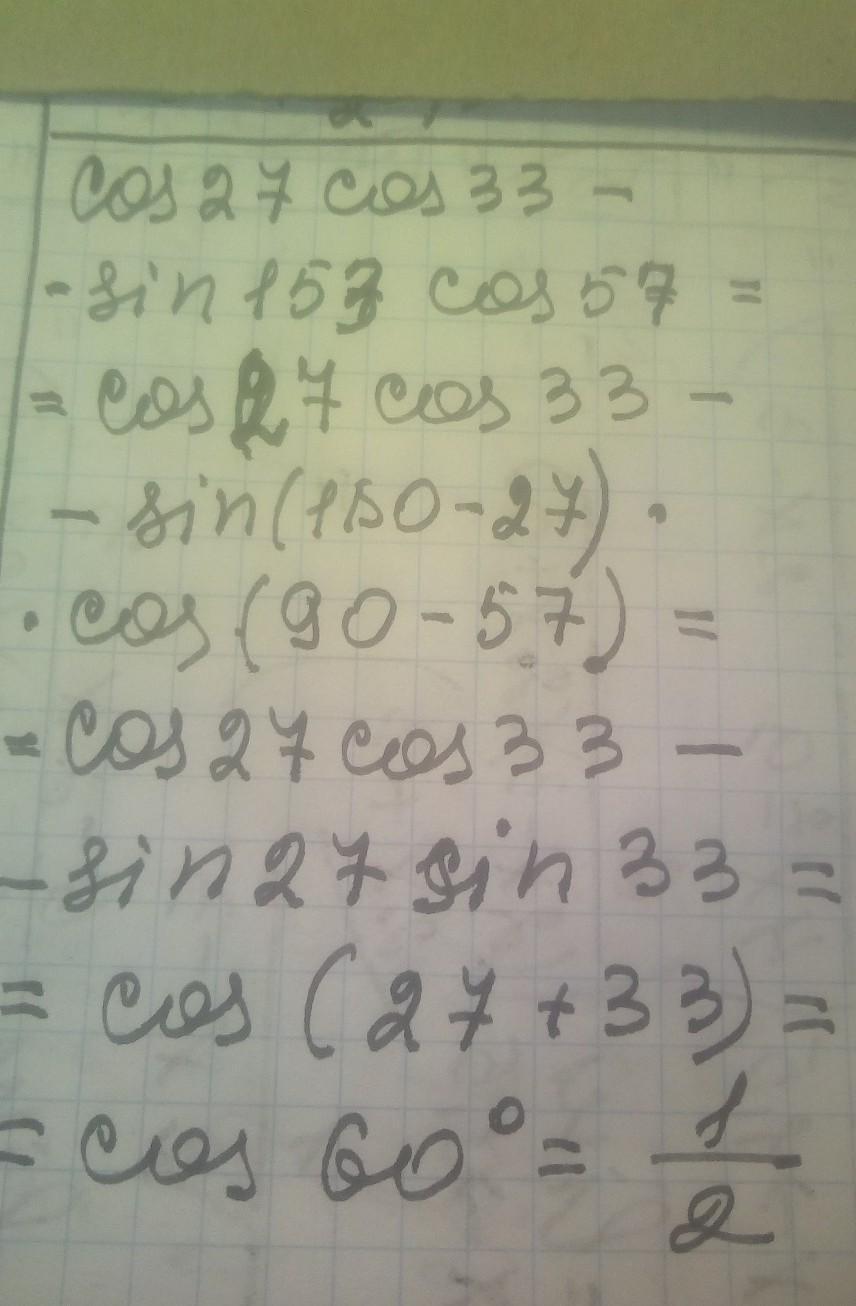
Автор ответа:
0
Похожие вопросы
Предмет: Українська мова,
автор: arianamih20
Предмет: Русский язык,
автор: aeldaniz
Предмет: География,
автор: imka16
Предмет: Математика,
автор: ver1981310