Предмет: Математика,
автор: ТимаTimaТима
Много баллов! Взять производную по всем правилам (Распишите полностью пожалуйста)
Приложения:
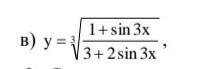
Ответы
Автор ответа:
1
Ответ:
ТимаTimaТима:
А как получился самый длинный числитель здесь?
немного непонятно
Скобки раскрыли, да?
да, а перед этим производная частного: (u'v-v'u)/v^2
понял, спасибо!!
а как конечное выражение получилось из предыдущего? Как (3+2sin(3x)) опускаем в знаменатель?
там степени сокращаются: в числителе была 2/3, в знаменателе 2. 2-2/3=4/3
А (1+sin(3x)) в знаменателе почему в квадрате?
сокращать это выражение не с чем, и степень остаётся прежняя: 2/3
Спасибо. Теперь до конца разобрался!
Похожие вопросы
Предмет: Физика,
автор: deniska34546
Предмет: Химия,
автор: anplehovaа
Предмет: Русский язык,
автор: король6757
Предмет: Биология,
автор: jasminezhak