Предмет: Математика,
автор: Geographist
Ещё один Интеграл! Для мозговитых людей! Буду благодарен!
Приложения:
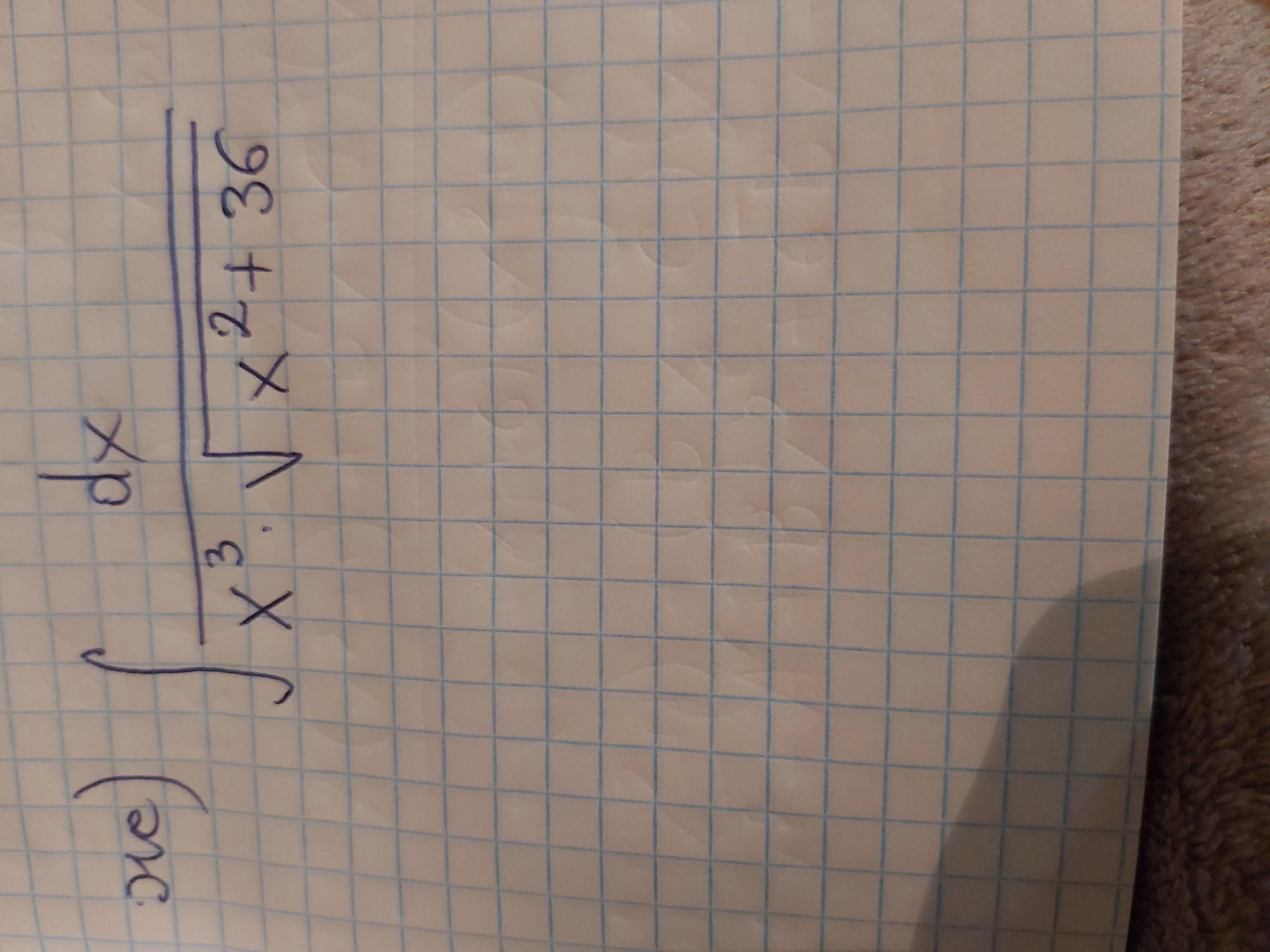
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Русский язык,
автор: Vasiliy2004
Предмет: Математика,
автор: danrurak99
Предмет: Химия,
автор: people07