Question

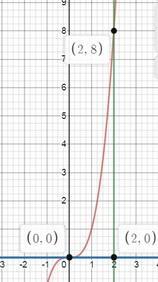
Обчисліть площу фігури обмеженої лініями y=x^3 y=0 x=2

Answer 1

Ответ:

Пошаговое объяснение:

y₁=x³; y₂=0; x=2

площадь фигуры равна

$S=\int\limits^a_b {(y_1-y_2)} \, dx$

у нас есть все, кроме одного из пределов интегрирования

найдем его. для этого найдем точки пересечения  y₁ и y₂

x³=0; ⇒  х=0

теперь

$S= \int\limits^2_0 {(x^3-0)} \, dx = \int\limits^2_0 {(x^3)} \, dx=\frac{x^4}{4} I_0^2=\frac{2^4}{4} -\frac{0^4}{4} =4$