Предмет: Математика,
автор: ПолинаLove15
Вычислить интеграл помогите решить пожалуйста
Приложения:
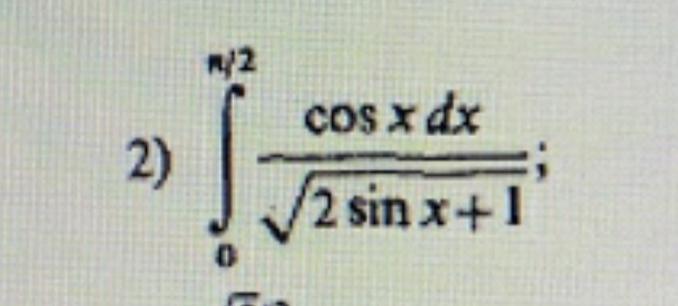
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Математика,
автор: Ольга454
Предмет: Литература,
автор: Drakylayrayes
Предмет: Обществознание,
автор: savenkova613013
Предмет: Математика,
автор: Олег11254
Предмет: Математика,
автор: maniken124214