Question

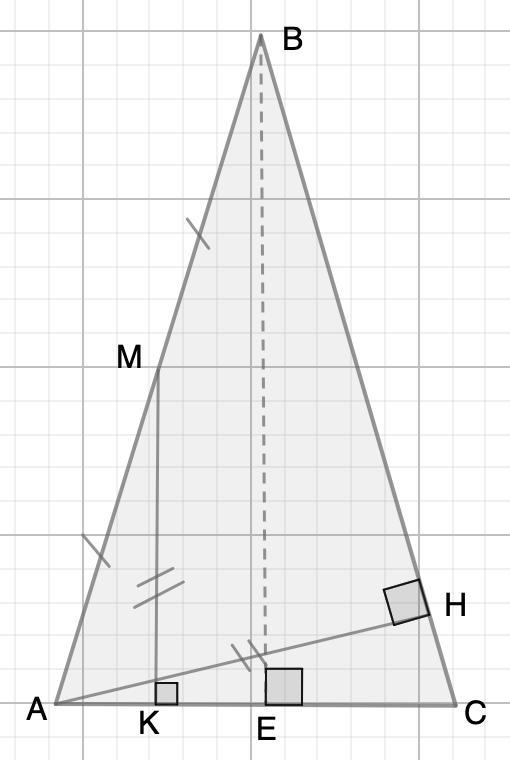
В равнобедренном треуголнике ABC (AB=BC) проведена высота АН, а из середины М стороны АВ опущен перпендикуляр МК на сорону АС. Оказалось, что АН=МК. Найдите периметр треугольника ABC, если АК=a.
СРОЧНО С ОБЪЯСНЕНИСЯ ПОЖАЛУЙСТА, МНОГО БАЛОЫ ДАЮ

Answer 1

Ответ:

20а

Объяснение:

Дано: АВС - равнобедренный;

АН - высота.

АМ=МВ; МК⊥АС;

АК=а

Найти: Р (ΔАВС)

Решение:

Проведем высоту ВЕ.

1. Рассмотрим ΔАМК и ΔАНС прямоугольные.

МК=АН (условие)

• Углы при основании равнобедренного треугольника равны.

⇒∠А=∠С

⇒ ΔАМК = ΔАНС (по катету и острому углу)

⇒ АМ=АС (как соответственные элементы)

2. Рассмотрим ΔАВЕ - прямоугольный.

• Если две прямые перпендикулярны третьей, то они параллельны между собой.

МК⊥АС; ВЕ⊥АС ⇒ МК || ВЕ

АМ=МВ (условие)

⇒ МК - средняя линия.

Тогда АК=КЕ=а или АЕ=2а

3. Рассмотрим ΔАВС - равнобедренный.

• В равнобедренном треугольнике высота является медианой.

⇒ АЕ=ЕВ=2а или АС=4а

4) АМ=АС=4а (п.1)

АМ=МВ =4а (условие) или АВ=8а

АВ=ВС=8а

• Периметр - сумма длин всех сторон.

Р (ΔАВС)=АВ+ВС+АС=8а+8а+4а=20а