Question

у некоторых параллелограммов даны их диагонали и сторона. Определите, какие параллелограммы являются ромбами1) d1=20, d2=48, a=26. 2) d1=32, d2=40,a=26. 3) d1=48,d2=14,a=25. 4) d1=14, d2=24,a=15. 5) d1=13,d2=15,a=17

Answer 1

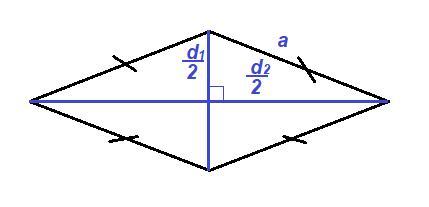
У ромба все стороны равны, диагонали пересекаются под прямым углом и точкой пересечения делятся пополам.

Значит, у ромба половинки диагоналей и сторона образуют прямоугольный треугольник. По теореме Пифагора в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Чтобы определить, является ли параллелограмм ромбом, достаточно проверить теорему Пифагора на одном из таких треугольников.

$\left(\dfrac{d_1}2\right)^2+\left(\dfrac{d_2}2\right)^2=a^2$

1) d1=20, d2=48, a=26.

$\left(\dfrac{20}2\right)^2+\left(\dfrac{48}2\right)^2=10^2+24^2=100+576=676=26^2$

 Параллелограмм 1) является ромбом.

2) d1=32, d2=40, a=26.

$\left(\dfrac{32}2\right)^2+\left(\dfrac{40}2\right)^2=16^2+20^2=256+400=656\neq26^2$

 Параллелограмм 2) не является ромбом.

3) d1=48,d2=14,a=25.

$\left(\dfrac{48}2\right)^2+\left(\dfrac{14}2\right)^2=24^2+7^2=576+49=625=25^2$

 Параллелограмм 3) является ромбом.

4) d1=14, d2=24,a=15.

$\left(\dfrac{14}2\right)^2+\left(\dfrac{24}2\right)^2=7^2+12^2=49+144=193\neq15^2$

 Параллелограмм 4) не является ромбом.

5) d1=13,d2=15,a=17

$\left(\dfrac{13}2\right)^2+\left(\dfrac{15}2\right)^2=\dfrac{169}4+\dfrac{225}4=\dfrac{394}4=98,5\neq17^2$

 Параллелограмм 5) не является ромбом.

Ответ: 1) и 3) параллелограммы являются ромбами.