Предмет: Математика,
автор: sefghregh
помогите пожалуйста!!!!!
Приложения:
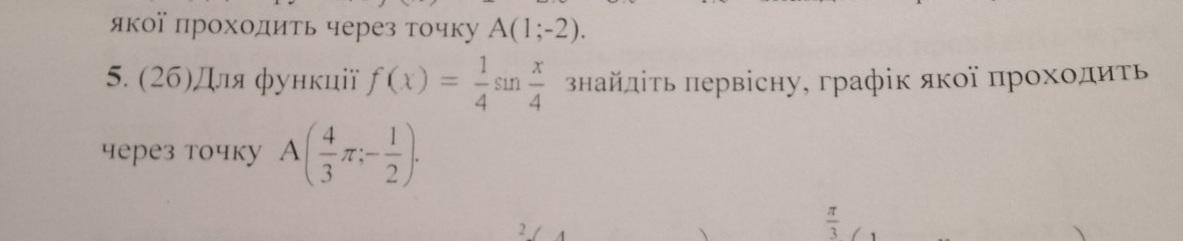
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
сперва ищем все семейство первообразных
теперь, чтобы найти С и определить конкретную первообразную, проходящую через точку А(3π/4; -1/2) подставим значение х =3π/4 и у = -1/2 в полученную формулу
C=0
первообразная имеет вид
Похожие вопросы
Предмет: Русский язык,
автор: usovaid
Предмет: Математика,
автор: влад515
Предмет: Русский язык,
автор: ep080978
Предмет: Физика,
автор: 37Zorky
Предмет: Литература,
автор: nuriza1308