Предмет: Математика,
автор: SennnnnnyK
Математика. Помогите, пожалуйста.
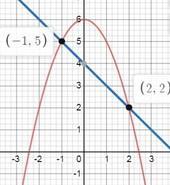
Рассчитайте содержание области, ограниченной кривыми y = 6 - x2 и x + y - 4 = 0. Нарисуйте иллюстративные рисунки.
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
y₁ = 6 - x²
х+у-4=0⇒ у= 4-х у₂=4-х
площадь фигуры равна значению определенного интеграла
сначала найдем пределы интегрирования, т.е. пересечение графиков функций y₁ и у₂
6-х² = 4-х
х² - х +2 = 0 ⇒ х₁ = -1; х₂ = 2 - это и есть пределы интегрирования
теперь считаем площадь
итак, ответ
S = 9/2
Приложения:
Похожие вопросы