Предмет: Математика,
автор: flash77779
Решить математику с фото.
Задание нужно расписать.
С 1 по 4 нужно решить.
В пятом нужно определить знак произведения функций.
Приложения:
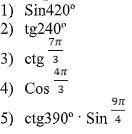
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: RUnannen
Предмет: Химия,
автор: ЗнатокБиологии
Предмет: Физика,
автор: petrakovalenks
Предмет: Математика,
автор: mussay86
Предмет: Химия,
автор: alydikaya2001